Next Page Previous Page Home Tools & Aids Search Handbook
5. Process Improvement
5.5. Advanced topics
5.5.9. An EDA approach to experimental design

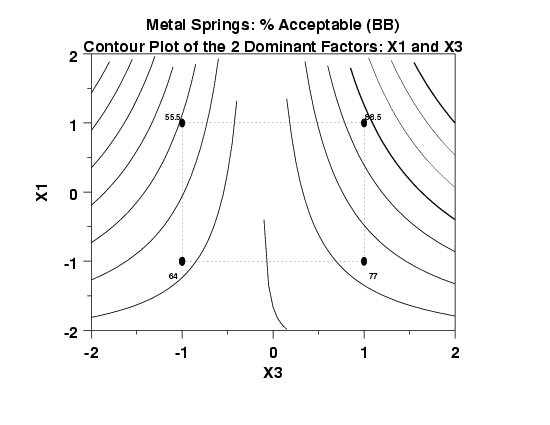
5.5.9.10.

DOE contour plot
Purpose The DOE contour plot answers the question:
    Where else could we have run the experiment to optimize the response?
Prior steps in this analysis have suggested the best setting for each of the k factors. These best settings may have been derived from
  1. Data: which of the n design points yielded the best response, and what were the settings of that design point, or from
  2. Averages: what setting of each factor yielded the best response "on the average".
This 10th (and last) step in the analysis sequence goes beyond the limitations of the n data points already chosen in the design and replaces the data-limited question
    "From among the n data points, what was the best setting?"
to a region-related question:
    "In general, what should the settings have been to optimize the response?"
Output The outputs from the DOE contour plot are
  1. Primary: Best setting (X10, X20, ..., Xk0) for each of the k factors. This derived setting should yield an optimal response.

  2. Secondary: Insight into the nature of the response surface and the importance/unimportance of interactions.
Definition A DOE contour plot is formed by
  • Vertical Axis: The second most important factor in the experiment.
  • Horizontal Axis: The most important factor in the experiment.
More specifically, the DOE contour plot is constructed and utilized via the following 7 steps:
  1. Axes
  2. Contour Curves
  3. Optimal Response Value
  4. Best Corner
  5. Steepest Ascent/Descent
  6. Optimal Curve
  7. Optimal Setting
with
  1. Axes: Choose the two most important factors in the experiment as the two axes on the plot.

  2. Contour Curves: Based on the fitted model and the best data settings for all of the remaining factors, draw contour curves involving the two dominant factors. This yields a graphical representation of the response surface. The details for constructing linear contour curves are given in a later section.

  3. Optimal Value: Identify the theoretical value of the response that constitutes "best." In particular, what value would we like to have seen for the response?

  4. Best "Corner": The contour plot will have four "corners" for the two most important factors Xi and Xj: (Xi, Xj) = (-, -), (-, +), (+, -), and (+, +). From the data, identify which of these four corners yields the highest average response \( \bar{Y} \).

  5. Steepest Ascent/Descent: From this optimum corner point, and based on the nature of the contour lines near that corner, step out in the direction of steepest ascent (if maximizing) or steepest descent (if minimizing).

  6. Optimal Curve: Identify the curve on the contour plot that corresponds to the ideal optimal value.

  7. Optimal Setting: Determine where the steepest ascent/descent line intersects the optimum contour curve. This point represents our "best guess" as to where we could have run our experiment so as to obtain the desired optimal response.
Motivation In addition to increasing insight, most experiments have a goal of optimizing the response. That is, of determining a setting (X10, X20, ..., Xk0) for which the response is optimized.

The tool of choice to address this goal is the DOE contour plot. For a pair of factors Xi and Xj, the DOE contour plot is a 2-dimensional representation of the 3-dimensional Y = f(Xi, Xj) response surface. The position and spacing of the isocurves on the DOE contour plot are an easily interpreted reflection of the nature of the surface.

In terms of the construction of the DOE contour plot, there are three aspects of note:

  1. Pairs of Factors: A DOE contour plot necessarily has two axes (only); hence only two out of the k factors can be represented on this plot. All other factors must be set at a fixed value (their optimum settings as determined by the ordered data plot, the DOE mean plot, and the interaction effects matrix plot).

  2. Most Important Factor Pair: Many DOE contour plots are possible. For an experiment with k factors, there are \( \left( \begin{array}{c} k \\ 2 \end{array} \right) \frac{k!} {2!(k-2)!} = \frac{k(k-1)}{2} \) possible contour plots. For example, for k = 4 factors there are 6 possible contour plots: X1 and X2, X1 and X3, X1 and X4, X2 and X3, X2 and X4, and X3 and X4. In practice, we usually generate only one contour plot involving the two most important factors.

  3. Main Effects Only: The contour plot axes involve main effects only, not interactions. The rationale for this is that the "deliverable" for this step is k settings, a best setting for each of the k factors. These k factors are real and can be controlled, and so optimal settings can be used in production. Interactions are of a different nature as there is no "knob on the machine" by which an interaction may be set to -, or to +. Hence the candidates for the axes on contour plots are main effects only--no interactions.
In summary, the motivation for the DOE contour plot is that it is an easy-to-use graphic that provides insight as to the nature of the response surface, and provides a specific answer to the question "Where (else) should we have collected the data so to have optimized the response?".
Plot for defective springs data Applying the DOE contour plot for the defective springs data set yields the following plot.

DOE contour plot for the defective springs data

How to interpret From the DOE contour plot for the defective springs data, we note the following regarding the 7 framework issues:
Conclusions for the defective springs data The application of the DOE contour plot to the defective springs data set results in the following conclusions:
  1. Optimal settings for the "next" run:

    Coded : (X1, X2, X3) = (+1.5, +1.0, +1.3)
    Uncoded: (OT, CC, QT) = (1637.5, 0.7, 127.5)

  2. Nature of the response surface:

    The X1*X3 interaction is important, hence the effect of factor X1 will change depending on the setting of factor X3.

Home Tools & Aids Search Handbook Previous Page Next Page