5.
Process Improvement
5.5.
Advanced topics
5.5.9.
An EDA approach to experimental design
5.5.9.10.
DOE contour plot
5.5.9.10.4.
|
How to Interpret: Best Corner
|
|
|
Four corners representing 2 levels for 2 factors
|
The contour plot will have four "corners" (two factors times two
settings per factor) for the two most important factors
Xi and Xj:
(Xi, Xj) = (-, -), (-, +), (+, -),
or (+, +). Which of these four corners yields the highest average
response 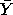 ? That is,
what is the "best corner"? ? That is,
what is the "best corner"?
|
|
Use the raw data
|
This is done by using the raw data, extracting out the two
"axes factors", computing the average response at each of the four
corners, then choosing the corner with the best average.
For the defective springs data, the raw data were
|
X1
|
X2
|
X3
|
Y
|
|
-
|
-
|
-
|
67
|
|
+
|
-
|
-
|
79
|
|
-
|
+
|
-
|
61
|
|
+
|
+
|
-
|
75
|
|
-
|
-
|
+
|
59
|
|
+
|
-
|
+
|
90
|
|
-
|
+
|
+
|
52
|
|
+
|
+
|
+
|
87
|
The two plot axes are X1 and X3 and so the relevant raw data collapses to
|
X1
|
X3
|
Y
|
|
-
|
-
|
67
|
|
+
|
-
|
79
|
|
-
|
-
|
61
|
|
+
|
-
|
75
|
|
-
|
+
|
59
|
|
+
|
+
|
90
|
|
-
|
+
|
52
|
|
+
|
+
|
87
|
|
|
Averages
|
which yields averages
|
X1
|
X3
|
Y
|
|
-
|
-
|
(67 + 61)/2 = 64
|
|
+
|
-
|
(79 + 75)/2 = 77
|
|
-
|
+
|
(59 + 52)/2 = 55.5
|
|
+
|
+
|
(90 + 87)/2 = 88.5
|
These four average values for the corners are annotated
on the plot. The best (highest) of these
values is 88.5. This comes from the (+, +) upper right corner. We
conclude that for the defective springs data the best corner is (+, +).
|
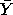 ? That is,
what is the "best corner"?
? That is,
what is the "best corner"?

