5.5. Advanced topics
5.5.9. An EDA approach to experimental design
5.5.9.4. |
Interaction effects matrix plot |
- What is the ranked list of factors (including 2-factor interactions), ranked from most important to least important; and
- What is the best setting for each of the k factors?
In practice, the most important interactions are likely to be 2-factor interactions. The total number of possible 2-factor interactions is \[ \left( \begin{array}{c} k \\ 2 \end{array} \right) = \frac{k!} {2!(k-2)!} = \frac{k(k-1)}{2} \] Thus for k = 3, the number of 2-factor interactions = 3, while for k = 7, the number of 2-factor interactions = 21.
It is important to distinguish between the number of interactions that are active in a given experiment versus the number of interactions that the analyst is capable of making definitive conclusions about. The former depends only on the physics and engineering of the problem. The latter depends on the number of factors, k, the choice of the k factors, the constraints on the number of runs, n, and ultimately on the experimental design that the analyst chooses to use. In short, the number of possible interactions is not necessarily identical to the number of interactions that we can detect.
Note that
- with full factorial designs, we can uniquely estimate interactions of all orders;
- with fractional factorial designs, we can uniquely estimate only some (or at times no) interactions; the more fractionated the design, the fewer interactions that we can estimate.
- Primary: Ranked list of the factors (including 2-factor
interactions) with the factors are ranked from important to
unimportant.
- Secondary: Best setting for each of the k factors.
In general, interactions are not the same as the usual (multiplicative) cross-products. However, for the special case of 2-level designs coded as (-, +) = (-1, +1), the interactions are identical to cross-products. By way of contrast, if the 2-level designs are coded otherwise (e.g., the (1, 2) notation espoused by Taguchi and others), then this equivalance is not true. Mathematically,
-
{-1, +1} x {-1, +1} => {-1, +1}
-
{1, 2} x {1, 2} => {1, 2, 4}
It is remarkable that with the - and + coding, the 2-factor interactions are dealt with, interpreted, and compared in the same way that the k main effects are handled. It is thus natural to include both 2-factor interactions and main effects within the same matrix plot for ease of comparison.
For the off-diagonal terms, the first construction step is to form the horizontal axis values, which will be the derived values (also - and +) of the cross-product. For example, the settings for the X1*X2 interaction are derived by simple multiplication from the data as shown below.
| X1 | X2 | X1*X2 |
| - | - | + |
| + | - | - |
| - | + | - |
| + | + | + |
After the entire X1*X2 vector of settings has been formed in this way, the vertical axis of the X1*X2 interaction plot is formed:
- the plot point above X1*X2 = "-" is simply the mean of all response values for which X1*X2 = "-"
- the plot point above X1*X2 = "+" is simply the mean of all response values for which X1*X2 = "+".
All the mean plots, for both main effects and 2-factor interactions, have a common scale to facilitate comparisons. Each mean plot has
- Vertical Axis: The mean response for a given setting (- or +)
of a given factor or a given 2-factor interaction.
- Horizontal Axis: The 2 settings (- and +) within each factor,
or within each 2-factor interaction.
- Legend:
- A tag (1, 2, ..., k, 12, 13, etc.), with
1 = X1, 2 = X2, ..., k =
Xk, 12 = X1*X2,
13 = X1*X3, 35 = X3*X5,
123 = X1*X2*X3, etc.) which
identifies the particular mean plot; and
- The least squares estimate of the factor (or 2-factor interaction) effect. These effect estimates are large in magnitude for important factors and near-zero in magnitude for unimportant factors.
- A tag (1, 2, ..., k, 12, 13, etc.), with
1 = X1, 2 = X2, ..., k =
Xk, 12 = X1*X2,
13 = X1*X3, 35 = X3*X5,
123 = X1*X2*X3, etc.) which
identifies the particular mean plot; and
-
\( Y = \mu + \beta_{1} X_{1} + \beta_{2} X_{2} + \beta_{12} X_{1} X_{2} +
\cdots + \epsilon \)
Thus, visually, the difference in the mean values on the plot is identically the least squares estimate for the effect. Large differences (steep lines) imply important factors while small differences (flat lines) imply unimportant factors.
- Important Factors (including 2-factor interactions);
- Best Settings;
- Confounding Structure (for fractional factorial designs).
- Important factors (including 2-factor interactions):
Jointly compare the k main factors and the k*(k-1)/2 2-factor interactions. For each of these subplots, as we go from the "-" setting to the "+" setting within a subplot, is there a shift in location of the average data (yes/no)? Since all subplots have a common (-1, +1) horizontal axis, questions involving shifts in location translate into questions involving steepness of the mean lines (large shifts imply steep mean lines while no shifts imply flat mean lines).
- Identify the factor or 2-factor interaction that has the
largest shift (based on averages). This defines
the "most important factor". The largest shift is
determined by the steepest line.
- Identify the factor or 2-factor interaction that has the
next largest shift (based on averages). This
defines the "second most important factor". This shift
is determined by the next steepest line.
- Continue for the remaining factors.
This ranking of factors and 2-factor interactions based on local means is a major step in building the definitive list of ranked factors as required for screening experiments.
- Identify the factor or 2-factor interaction that has the
largest shift (based on averages). This defines
the "most important factor". The largest shift is
determined by the steepest line.
- Best settings:
For each factor (of the k main factors along the diagonal), which setting (- or +) yields the "best" (highest/lowest) average response?
Note that the experimenter has the ability to change settings for only the k main factors, not for any 2-factor interactions. Although a setting of some 2-factor interaction may yield a better average response than the alternative setting for that same 2-factor interaction, the experimenter is unable to set a 2-factor interaction setting in practice. That is to say, there is no "knob" on the machine that controls 2-factor interactions; the "knobs" only control the settings of the k main factors.
How then does this matrix of subplots serve as an improvement over the k best settings that one would obtain from the DOE mean plot? There are two common possibilities:
- Steep Line:
For those main factors along the diagonal that have steep lines (that is, are important), choose the best setting directly from the subplot. This will be the same as the best setting derived from the DOE mean plot.
- Flat line:
For those main factors along the diagonal that have flat lines (that is, are unimportant), the naive conclusion to use either setting, perhaps giving preference to the cheaper setting or the easier-to-implement setting, may be unwittingly incorrect. In such a case, the use of the off-diagonal 2-factor interaction information from the interaction effects matrix is critical for deducing the better setting for this nominally "unimportant" factor.
To illustrate this, consider the following example:
- Suppose the factor X1 subplot is steep (important) with the best setting for X1 at "+".
- Suppose the factor X2 subplot is flat (unimportant) with both settings yielding about the same mean response.
Then what setting should be used for X2? To answer this, consider the following two cases:
- Case 1. If the X1*X2 interaction plot happens also to be flat (unimportant), then choose either setting for X2 based on cost or ease.
- Case 2. On the other hand, if the X1*X2 interaction plot is steep (important), then this dictates a prefered setting for X2 not based on cost or ease.
To be specific for case 2, if X1*X2 is important, with X1*X2 = "+" being the better setting, and if X1 is important, with X1 = "+" being the better setting, then this implies that the best setting for X2 must be "+" (to assure that X1*X2 (= +*+) will also be "+"). The reason for this is that since we are already locked into X1 = "+", and since X1*X2 = "+" is better, then the only way we can obtain X1*X2 = "+" with X1 = "+" is for X2 to be "+" (if X2 were "-", then X1*X2 with X1 = "+" would yield X1*X2 = "-").
In general, if X1 is important, X1*X2 is important, and X2 is not important, then there are four distinct cases for deciding what the best setting is for X2:
X1 X1*X2 => X2 + + + + - - - + - - - + -
(x1best, x2best, ..., xkbest)
This average-based k-vector should be compared with best settings k-vectors obtained from previous steps (in particular, from step 1 in which the best settings were drawn from the best data value).
When the average-based best settings and the data-based best settings agree, we benefit from the increased confidence given our conclusions.
When the average-based best settings and the data-based best settings disagree, then what settings should the analyst finally choose? Note that in general the average-based settings and the data-based settings will invariably be identical for all "important" factors. Factors that do differ are virtually always "unimportant". Given such disagreement, the analyst has three options:
- Use the average-based settings for minor factors. This has the advantage of a broader (average) base of support.
- Use the data-based settings for minor factors. This has the advantage of demonstrated local optimality.
- Use the cheaper or more convenient settings for the local factor. This has the advantage of practicality.
Thus the interaction effects matrix yields important information not only about the ranked list of factors, but also about the best settings for each of the k main factors. This matrix of subplots is one of the most important tools for the experimenter in the analysis of 2-level screening designs.
- Steep Line:
- Confounding Structure (for Fractional Factorial Designs)
When the interaction effects matrix is used to analyze 2-level fractional (as opposed to full) factorial designs, important additional information can be extracted from the matrix regarding confounding structure.
It is well-known that all fractional factorial designs have confounding, a property whereby every estimated main effect is confounded/contaminated/biased by some high-order interactions. The practical effect of this is that the analyst is unsure of how much of the estimated main effect is due to the main factor itself and how much is due to some confounding interaction. Such contamination is the price that is paid by examining k factors with a sample size n that is less than a full factorial n = 2k runs.
It is a "fundamental theorem" of the discipline of experimental design that for a given number of factors k and a given number of runs n, some fractional factorial designs are better than others. "Better" in this case means that the intrinsic confounding that must exist in all fractional factorial designs has been minimized by the choice of design. This minimization is done by constructing the design so that the main effect confounding is pushed to as high an order interaction as possible.
The rationale behind this is that in physical science and engineering systems it has been found that the "likelihood" of high-order interactions being significant is small (compared to the likelihood of main effects and 2-factor interactions being significant). Given this, we would prefer that such inescapable main effect confounding be with the highest order interaction possible, and hence the bias to the estimated main effect be as small as possible.
The worst designs are those in which the main effect confounding is with 2-factor interactions. This may be dangerous because in physical/engineering systems, it is quite common for Nature to have some real (and large) 2-factor interactions. In such a case, the 2-factor interaction effect will be inseparably entangled with some estimated main effect, and so the experiment will be flawed in that
- ambiguous estimated main effects and
- an ambiguous list of ranked factors
will result.
If the number of factors, k, is large and the number of runs, n, is constrained to be small, then confounding of main effects with 2-factor interactions is unavoidable. For example, if we have k = 7 factors and can afford only n = 8 runs, then the corresponding 2-level fractional factorial design is a 27-4 which necessarily will have main effects confounded with (3) 2-factor interactions. This cannot be avoided.
On the other hand, situations arise in which 2-factor interaction confounding with main effects results not from constraints on k or n, but on poor design construction. For example, if we have k = 7 factors and can afford n = 16 runs, a poorly constructed design might have main effects counfounded with 2-factor interactions, but a well-constructed design with the same k = 7, n = 16 would have main effects confounded with 3-factor interactions but no 2-factor interactions. Clearly, this latter design is preferable in terms of minimizing main effect confounding/contamination/bias.
For those cases in which we do have main effects confounded with 2-factor interactions, an important question arises:
-
For a particular main effect of interest,
how do we know which 2-factor interaction(s)
confound/contaminate that main effect?
The usual answer to this question is by means of generator theory, confounding tables, or alias charts. An alternate complementary approach is given by the interaction effects matrix. In particular, if we are examining a 2-level fractional factorial design and
- if we are not sure that the design has main effects confounded with 2-factor interactions, or
- if we are sure that we have such 2-factor interaction confounding but are not sure what effects are confounded,
then how can the interaction effects matrix be of assistance? The answer to this question is that the confounding structure can be read directly from the interaction effects matrix.
For example, for a 7-factor experiment, if, say, the factor X3 is confounded with the 2-factor interaction X2*X5, then
- the appearance of the factor X3 subplot and the appearance of the 2-factor interaction X2*X5 subplot will necessarily be identical, and
- the value of the estimated main effect for X3 (as given in the legend of the main effect subplot) and the value of the estimated 2-factor interaction effect for X2*X5 (as given in the legend of the 2-factor interaction subplot) will also necessarily be identical.
The above conditions are necessary, but not sufficient for the effects to be confounded.
Hence, in the abscence of tabular descriptions (from your statistical software program) of the confounding structure, the interaction effect matrix offers the following graphical alternative for deducing confounding structure in fractional factorial designs:
- scan the main factors along the diagonal subplots and choose the subset of factors that are "important".
- For each of the "important" factors, scan all of the 2-factor interactions and compare the main factor subplot and estimated effect with each 2-factor interaction subplot and estimated effect.
- If there is no match, this implies that the main effect is not confounded with any 2-factor interaction.
- If there is a match, this implies that the main effect may be confounded with that 2-factor interaction.
- If none of the main effects are confounded with any 2-factor interactions, we can have high confidence in the integrity (non-contamination) of our estimated main effects.
- In practice, for highly-fractionated designs, each main effect may be confounded with several 2-factor interactions. For example, for a 27-4 fractional factorial design, each main effect will be confounded with three 2-factor interactions. These 1 + 3 = 4 identical subplots will be blatantly obvious in the interaction effects matrix.
Finally, what happens in the case in which the design the main effects are not confounded with 2-factor interactions (no diagonal subplot matches any off-diagonal subplot). In such a case, does the interaction effects matrix offer any useful further insight and information?
The answer to this question is yes because even though such designs have main effects unconfounded with 2-factor interactions, it is fairly common for such designs to have 2-factor interactions confounded with one another, and on occasion it may be of interest to the analyst to understand that confounding. A specific example of such a design is a 24-1 design formed with X4 settings = X1*X2*X3. In this case, the 2-factor-interaction confounding structure may be deduced by comparing all of the 2-factor interaction subplots (and effect estimates) with one another. Identical subplots and effect estimates hint strongly that the two 2-factor interactions are confounded. As before, such comparisons provide necessary (but not sufficient) conditions for confounding. Most statistical software for analyzing fractional factorial experiments will explicitly list the confounding structure.
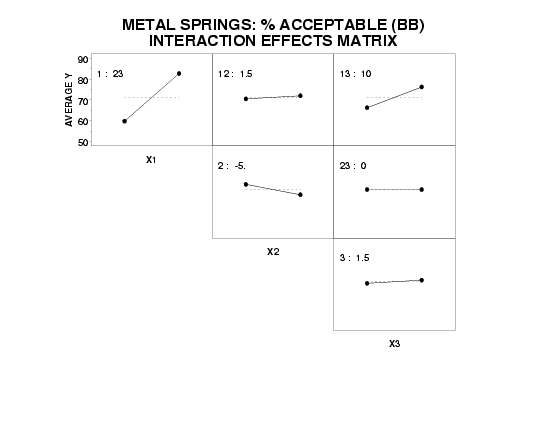
- Ranked list of factors (including 2-factor interactions):
- X1 (estimated effect = 23.0)
- X1*X3 (estimated effect = 10.0)
- X2 (estimated effect = -5.0)
- X3 (estimated effect = 1.5)
- X1*X2 (estimated effect = 1.5)
- X2*X3 (estimated effect = 0.0)
Factor 1 definitely looks important. The X1*X3 interaction looks important. Factor 2 is of lesser importance. All other factors and 2-factor interactions appear to be unimportant.
- Best Settings (on the average):
-
(X1, X2, X3) = (+, -, +) = (+1, -1, +1)