SLOPDF

SLOPDF (LET)

Library Function

Compute the slope probability density function with shape parameter .

The standard slope distribution has the following probability density function:

with denoting the shape parameter.

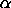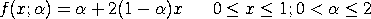
This distribution can be extended with lower and upper bound parameters. If a and b denote the lower and upper bounds, respectively, then the location and scale parameters are:

location = a
scale = b - a

The general form of the distribution can then be found by using the relation

LET <y> = SLOPDF(<x>,<alpha>,<a>,<b>)
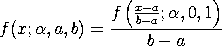
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable containing values in the interval (a,b);
            <y> is a variable or a parameter (depending on what <x> is) where the computed slope pdf value is stored;
            <alpha> is a positive number, parameter, or variable that specifies the shape parameter;
            <a> is a number, parameter, or variable that specifies the lower limit;
            <b> is a number, parameter, or variable that specifies the upper limit;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <a> and <b> are omitted, they default to 0 and 1, respectively.

LET A = SLOPDF(0.3,0.2)
LET Y = SLOPDF(X,0.5,0,5)
PLOT SLOPDF(X,2,0,3) FOR X = 0 0.01 3

Slope random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET ALPHA = <value>
LET A = <value>
LET B = <value>
LET Y = SLOPE RANDOM NUMBERS FOR I = 1 1 N
SLOPE PROBABILITY PLOT Y
SLOPE PROBABILITY PLOT Y2 X2
SLOPE PROBABILITY PLOT Y3 XLOW XHIGH
SLOPE KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
SLOPE CHI-SQUARE GOODNESS OF FIT Y2 X2
SLOPE CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH


The following commands can be used to estimate the alpha shape parameter for the slope distribution:

LET ALPHA1 = <value>
LET ALPHA2 = <value>
SLOPE PPCC PLOT Y
SLOPE PPCC PLOT Y2 X2
SLOPE PPCC PLOT Y3 XLOW XHIGH
SLOPE KS PLOT Y
SLOPE KS PLOT Y2 X2
SLOPE KS PLOT Y3 XLOW XHIGH


The default values for ALPHA1 and ALPHA2 are 0.05 and 2.

The probability plot can then be used to estimate the lower and upper limits (lower limit = PPA0, upper limit = PPA0 + PPA1).

For the ks plot, we can fix the location and scale. This is equivalent to assuming that the lower and upper limits are known (e.g., we could use the data minimum and maximum as the lower and upper limit values). Given that the lower and upper limits are LOWLIM and UPPLIM, enter the commands

LET KSLOC = LOWLIM
LET KSSCALE = UPPLIM


The ppcc plot is invariant to location and scale, so we cannot fix the lower and upper limits.

The BOOTSTRAP DISTRIBUTION command can be used to find uncertainty intervals for the ppcc plot and ks plot.

None

None

SLOCDF	= Compute the slope cumulative distribution function.
SLOPPF	= Compute the slope percent point function.
TSSPDF	= Compute the two-sided slope probability density function.
OGIPDF	= Compute the ogive probability density function.
TOPPDF	= Compute the Topp and Leone probability density function.
RGTPDF	= Compute the generalized reflected slope probability density function.
GTLPDF	= Compute the generalized slope probability density function.
TSPPDF	= Compute the two-sided power probability density function.
BETPDF	= Compute the alpha probability density function.
TRIPDF	= Compute the triangular probability density function.
TRAPDF	= Compute the trapezoid probability density function.
UNIPDF	= Compute the uniform probability density function.
POWPDF	= Compute the power probability density function.
JSBPDF	= Compute the Johnson SB probability density function.

Samuel Kotz and J. Rene Van Dorp 2004, "Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications", World Scientific, chapter 8.

Distributional Modeling

2007/10

 
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
LET ALPHA  = 0.5
TITLE Alpha = ^alpha
PLOT SLOPDF(X,ALPHA) FOR X = 0  0.01  1
.
LET ALPHA  = 1
TITLE Alpha = ^alpha
PLOT SLOPDF(X,ALPHA) FOR X = 0  0.01  1
.
LET ALPHA  = 1.5
TITLE Alpha = ^alpha
PLOT SLOPDF(X,ALPHA) FOR X = 0  0.01  1
.
LET ALPHA  = 2
TITLE Alpha = ^alpha
PLOT SLOPDF(X,ALPHA) FOR X = 0  0.01  1
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Slope Probability Density Functions
    

 
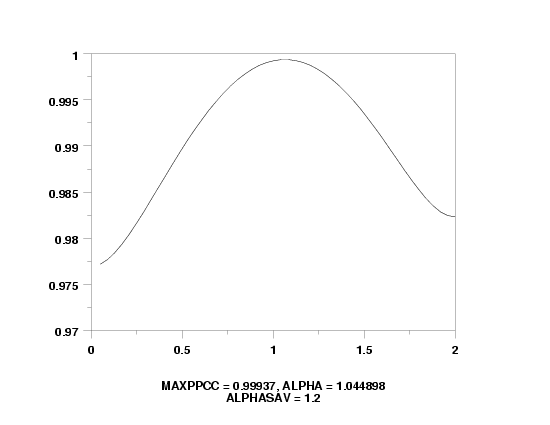
let alpha = 1.2
let y = slope rand numb for i = 1 1 200
.
let alphasav = alpha
slope ppcc plot y
just center
move 50 5
let alpha = shape
text maxppcc = ^maxppcc, Alpha = ^alpha
move 50 2
text Alphasav = ^alphasav
.
char x
line blank
slope prob plot y
move 50 5
text PPA0 = ^ppa0, PPA1 = ^ppa1
move 50 2
let upplim = ppa0 + ppa1
text Lower Limit = ^ppa0, Upper Limit = ^upplim
char blank
line solid
.
let ksloc = ppa0
let ksscale = upplim
slope kolm smir goodness of fit y
    





                   KOLMOGOROV-SMIRNOV GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            SLOPE
    NUMBER OF OBSERVATIONS              =      200
  
 TEST:
 KOLMOGOROV-SMIRNOV TEST STATISTIC      =   0.3355396E-01
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       0.086*              ACCEPT H0
                      0.085**
             5%       0.096*              ACCEPT H0
                      0.095**
             1%       0.115*              ACCEPT H0
                      0.114**
  
     *  - STANDARD LARGE SAMPLE APPROXIMATION  ( C/SQRT(N) )
    ** - MORE ACCURATE LARGE SAMPLE APPROXIMATION  ( C/SQRT(N + SQRT(N/10)) )