

|
GTLPDFName:
 and
and
 . .
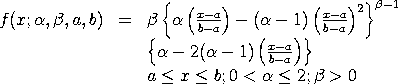
with
The case where a = 0 and b = 1 is referred to as the standard generalized Topp and Leone distribution. It has the following probability density function:
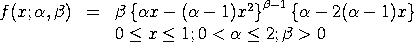
The lower and upper limits are related to the location and scale parameters as follows:
scale = b - a Kotz and van Dorp have proposed this distribution as an alternative to the beta distribution.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing values in the interval (a,b); <y> is a variable or a parameter (depending on what <x> is) where the computed generalized Topp and Leone pdf value is stored; <alpha> is a number, parameter, or variable in the interval (0, 2) that specifies the first shape parameter; <beta> is a positive number, parameter, or variable that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower limit; <b> is a number, parameter, or variable that specifies the upper limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
LET Y = GTLPDF(X,0.5,2) PLOT GTLPDF(X,2,3) FOR X = 0 0.01 1
LET BETA = <value> LET A = <value> LET B = <value> LET Y = GENERALIZED TOPP LEONE ... RANDOM NUMBERS FOR I = 1 1 N GENERALIZED TOPP LEONE PROBABILITY PLOT Y GENERALIZED TOPP LEONE PROBABILITY PLOT Y2 X2 GENERALIZED TOPP LEONE PROBABILITY PLOT Y3 XLOW XHIGH GENERALIZED TOPP LEONE ... KOLMOGOROV SMIRNOV GOODNESS OF FIT Y GENERALIZED TOPP LEONE CHI-SQUARE GOODNESS OF FIT Y2 X2 GENERALIZED TOPP LEONE CHI-SQUARE ... GOODNESS OF FIT Y3 XLOW XHIGH
The following commands can be used to estimate the
LET ALPHA2 = <value>$ LET BETA1 = <value>$ LET BETA2 = <value>$ GENERALIZED TOPP LEONE PPCC PLOT Y$ GENERALIZED TOPP LEONE PPCC PLOT Y2 X2$ GENERALIZED TOPP LEONE PPCC PLOT Y3 XLOW XHIGH$ GENERALIZED TOPP LEONE KS PLOT Y$ GENERALIZED TOPP LEONE KS PLOT Y2 X2$ GENERALIZED TOPP LEONE KS PLOT Y3 XLOW XHIGH$ The default values for ALPHA1 and ALPHA2 are 0.1 and 2. The default values for BETA1 and BETA2 are 0.5 and 10. The probability plot can then be used to estimate the lower and upper limits (lower limit = PPA0, upper limit = PPA0 + PPA1). The following options may be useful for these commands.
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
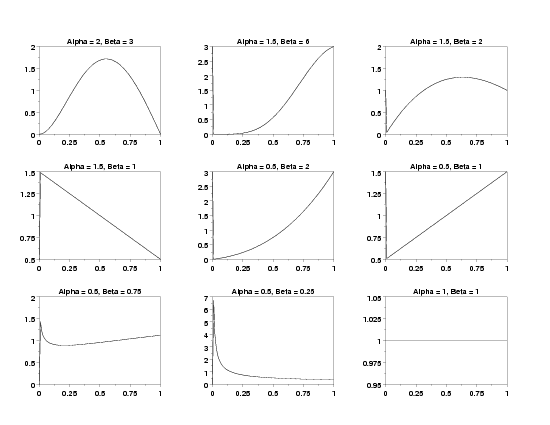
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
.
LET ALPHA = 2
LET BETA = 3
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 6
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.75
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.25
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT GTLPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
END OF MULTIPLOT
 Program 2:
Program 2:
let alpha = 1.5
let beta = 2
.
let y = generalized topp leone rand numb for i = 1 1 200
.
let alphsav = alpha
let betasav = beta
generalized topp leone ppcc plot y
just center
move 50 5
let alpha = shape1
let beta = shape2
text maxppcc = ^maxppcc, Alpha = ^alpha, Beta = ^beta
move 50 2
text Alphasav = ^alphsav, Betasav = ^betasav
.
char x
line blank
generalized topp leone prob plot y
move 50 5
text PPA0 = ^ppa0, PPA1 = ^ppa1
move 50 2
let upplim = ppa0 + ppa1
text Lower Limit = ^ppa0, Upper Limit = ^upplim
char blank
line solid
.
let ksloc = ppa0
let ksscale = upplim
generalized topp leone kolm smir goodness of fit y
.
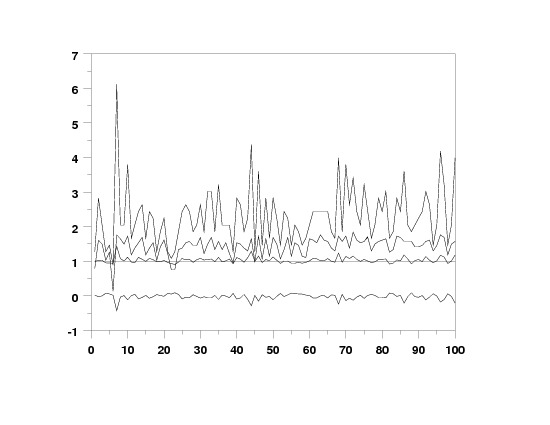
bootstrap generalized topp leone plot y
The following output is generated:
KOLMOGOROV-SMIRNOV GOODNESS-OF-FIT TEST
NULL HYPOTHESIS H0: DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION: GENERALIZED TOPP AND LEONE
NUMBER OF OBSERVATIONS = 200
TEST:
KOLMOGOROV-SMIRNOV TEST STATISTIC = 1.000000
ALPHA LEVEL CUTOFF CONCLUSION
10% 0.086* REJECT H0
0.085**
5% 0.096* REJECT H0
0.095**
1% 0.115* REJECT H0
0.114**
* - STANDARD LARGE SAMPLE APPROXIMATION ( C/SQRT(N) )
** - MORE ACCURATE LARGE SAMPLE APPROXIMATION ( C/SQRT(N + SQRT(N/10)) )
Date created: 9/10/2007 |