|
|
RGTPDFName:
and
 .
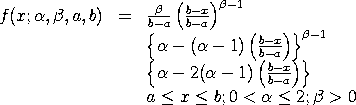
with
The case where a = 0 and b = 1 is referred to as the standard reflected generalized Topp and Leone distribution. The lower and upper limits are related to the location and scale parameters as follows:
scale = b - a Kotz and van Dorp have proposed this distribution as an alternative to the beta distribution. It is distinguished from the beta distribution in that it can have positive density at the lower limit with a strict positive mode.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing values in the interval (a,b); <y> is a variable or a parameter (depending on what <x> is) where the computed reflected generalized Topp and Leone pdf value is stored; <alpha> is a number, parameter, or variable in the interval (0, 2) that specifies the first shape parameter; <beta> is a positive number, parameter, or variable that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower limit; <b> is a number, parameter, or variable that specifies the upper limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
LET Y = RGTPDF(X,0.5,2) PLOT RGTPDF(X,2,3) FOR X = 0 0.01 1
LET BETA = <value> LET A = <value> LET B = <value> LET Y = REFLECTED GENERALIZED TOPP LEONE ... RANDOM NUMBERS FOR I = 1 1 N REFLECTED GENERALIZED TOPP LEONE PROBABILITY PLOT Y REFLECTED GENERALIZED TOPP LEONE PROBABILITY PLOT Y2 X2 REFLECTED GENERALIZED TOPP LEONE PROBABILITY PLOT ... Y3 XLOW XHIGH REFLECTED GENERALIZED TOPP LEONE ... KOLMOGOROV SMIRNOV GOODNESS OF FIT Y REFLECTED GENERALIZED TOPP LEONE CHI-SQUARE ... GOODNESS OF FIT Y2 X2 REFLECTED GENERALIZED TOPP LEONE CHI-SQUARE ... GOODNESS OF FIT Y3 XLOW XHIGH
The following commands can be used to estimate the
LET ALPHA2 = <value>$ LET BETA1 = <value>$ LET BETA2 = <value>$ REFLECTED GENERALIZED TOPP LEONE PPCC PLOT Y$ REFLECTED GENERALIZED TOPP LEONE PPCC PLOT Y2 X2$ REFLECTED GENERALIZED TOPP LEONE PPCC PLOT Y3 XLOW XHIGH$ REFLECTED GENERALIZED TOPP LEONE KS PLOT Y$ REFLECTED GENERALIZED TOPP LEONE KS PLOT Y2 X2$ REFLECTED GENERALIZED TOPP LEONE KS PLOT Y3 XLOW XHIGH$ The default values for ALPHA1 and ALPHA2 are 0.1 and 2. The default values for BETA1 and BETA2 are 0.5 and 10. The probability plot can then be used to estimate the lower and upper limits (lower limit = PPA0, upper limit = PPA0 + PPA1). The following options may be useful for these commands.
Kotz and Van Dorp describe an approximate maximum likelihood
method for estimating the
The parameter
![G(alpha) = {N/SUM[i=1 to m][n(i)*LOG(1/(alpha*y(i) -
(alpha - 1)*y(i)^2)]) - 1}*
SUM[i=1 to m][n(i)*(1 - y(i)/(alpha - (alpha - 1)*y(i))] +
SUM[i=1 to m][n(i)*(1 - 2*y(i)/(alpha - 2*(alpha - 1)*y(i))]](eqns/rgtml1.gif)
where
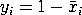
The maximum likelihood estimate of
![betahat = N/{SUM[i=1 to m][n(i)*LOG(1/(alpha*y(i)-(alpha-1)*y(i)^2))]](eqns/rgtml2.gif)
If the data lie outside the (0,1) interval, then we first apply the transformation
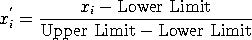
To generate the approximate maximum likelihood estimates for ungrouped data in Dataplot, enter the command
For grouped data, enter one of the following commands
REFLECTED GENERALIZED TOPP AND LEONE MLE Y XLOW XHIGH In the first case, X denotes the mid-points of the bins and Y denotes the corresponding frequency. In the second case, XLOW denotes the lower end-points of the bins and XHIGH denotes the upper end-points of the bins. If the lower and upper limits are fixed and known, you can enter the following commands:
LET UPPLIMIT = <VALUE> For the unknown case, the minimum and maximum of the data will be used (an epsilon value will be subtracted/added to the minimum/maximum). Alternatively, you can use the estimates of the lower/upper limits generated by either the PPCC plot method or the KS plot methods and specify the LOWLIMIT and UPPLIMIT as above.
To specify starting values for
LET BETASV = <VALUE> For example, the estimates obtained from the PPCC plot or the KS plot can be used as starting values for the maximum likelihood estimates.
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
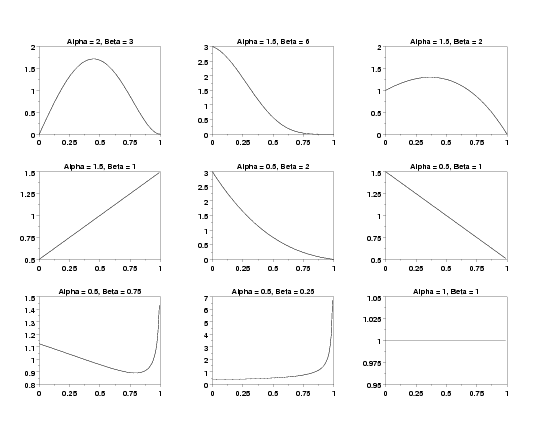
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
.
LET ALPHA = 2
LET BETA = 3
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 6
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.75
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.25
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
END OF MULTIPLOT
Program 2:
let alpha = 1.5
let beta = 2
.
let y = reflected generalized topp leone rand numb for i = 1 1 200
.
let alphsav = alpha
let betasav = beta
reflected generalized topp leone ppcc plot y
just center
move 50 5
let alpha = shape1
let beta = shape2
text maxppcc = ^maxppcc, Alpha = ^alpha, Beta = ^beta
move 50 2
text Alphasav = ^alphsav, Betasav = ^betasav
.
char x
line blank
reflected generalized topp leone prob plot y
move 50 5
text PPA0 = ^ppa0, PPA1 = ^ppa1
move 50 2
let upplim = ppa0 + ppa1
text Lower Limit = ^ppa0, Upper Limit = ^upplim
char blank
line solid
.
let ksloc = ppa0
let ksscale = upplim
reflected generalized topp leone kolm smir goodness of fit y
.
bootstrap reflected generalized topp leone plot y
The following output is generated:
Date created: 9/10/2007 |
.
For unbinned data, the intervals consist of the individual
observations (and the frequency is equal to 1). The total
sample size, N is the sum of the ni.
