PAPPDF

PAPPDF (LET)

Library Function

Compute the Polya-Aeppli probability mass function.

The formula for the Polya-Aeppli probability mass function is
\( \begin{array}{lcll} p(x;\theta,p) & = & e^{-\theta} \hspace{0.3in} & x = 0 \\ & = & e^{-\theta} p^{x} \sum_{j=1}^{x} {\left( \begin{array}{c} x - 1 \\ j-1 \end{array} \right) \frac{(\theta(1-p)/p)^j}{j!}} \hspace{0.3in} & x = 1, 2, \cdots \\ & & 0 < p < 1; \theta > 0 & \end{array} \)

with \( \theta \) and p denoting the shape parameters.

The Polya-Aeppli distribution can be derived as a model for the number of objects where the objects occur in clusters, the clusters follow a Poisson distribution with shape parameter \( \theta \), and the number of objects within a cluster follows a geometric distribution with shape parameter p. For this reason, this distribution is sometimes referred to as a geometric Poisson distribution

Note that there are a number of alternative parameterizations of this distribution in the literature. The parameterization used above is the one given in Johnson, Kotz, and Kemp.

The moments of this distribution are:

mean	=	\( \frac{\theta}{1-p} \)
variance	=	\( \frac{\theta(1+p)}{(1-p)^2} \)
skewness	=	\( \frac{(1 + 4 + p^2)^2}{(1+p)^3 \theta} \)
kurtosis	=	\( 3 + \frac{1+11p + 11p^2 + p^3} {(1+p)^2 \theta} \)

LET <y> = PAPPDF(<x>,<theta>,<p>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative integer variable, number, or parameter;
            <theta> is a positive number or parameter that specifies the first shape parameter;
            <p> is a positive number or parameter that specifies the second shape parameter;
            <y> is a variable or a parameter where the computed Polya-Aeppli pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = PAPPDF(3,3,0.5)
LET Y = PAPPDF(X1,2,0.3)
PLOT PAPPDF(X,2,0.3) FOR X = 0 1 20

For a number of commands utilizing the Polya-Aeppli distribution, it is convenient to bin the data. There are two basic ways of binning the data.
1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:
   LET AMIN = MINIMUM Y
   LET AMAX = MAXIMUM Y
   LET AMIN2 = AMIN - 0.5
   LET AMAX2 = AMAX + 0.5
   CLASS MINIMUM AMIN2
   CLASS MAXIMUM AMAX2
   CLASS WIDTH 1
   LET Y2 X2 = BINNED
   

2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands
   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
   

   If you already have equal width bins data, you can use the commands

   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
   

   The MINSIZE parameter defines the minimum class frequency. The default value is 5.

You can generate Polya-Aeppli random numbers, probability plots, and chi-square goodness of fit tests with the following commands:
LET N = VALUE
LET THETA = <value>
LET LAMBDA = <value>
LET Y = POLYA AEPPLI RANDOM NUMBERS FOR I = 1 1 N


POLYA AEPPLI PROBABILITY PLOT Y
POLYA AEPPLI PROBABILITY PLOT Y2 X2
POLYA AEPPLI PROBABILITY PLOT Y3 XLOW XHIGH


POLYA AEPPLI CHI-SQUARE GOODNESS OF FIT Y2 X2
POLYA AEPPLI CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH


To obtain the method of moments, the method of zero frequency and the mean, and the weighted discrepancies estimates of lambda and theta, enter the command

POLYA AEPPLI MAXIMUM LIKELIHOOD Y
POLYA AEPPLI MAXIMUM LIKELIHOOD Y2 X2


The method of moments estimators are:

\( \hat{\theta} = \frac{2\bar{x}^2}{s^2 + \bar{x}} \)

\( \hat{p} = \frac{s^2 - \bar{x}} {s^2 + \bar{x}} \)

with \( \bar{x} \) and s² denoting the sample mean and sample variance, respectively.

The method of zero frequency and sample mean estimators are:

\( \hat{\theta} = -\log \left( \frac{f_0}{N} \right) \)

\( \hat{p} = 1 - \frac{\hat{\theta}} {\bar{x}} \)

with \( \bar{x} \) and f₀ denoting the sample mean and sample frequency at x = 0, respectively.

The method of the first two frequencies estimators are:

\( \hat{\theta} = -\log \left( \frac{f_0}{N} \right) \)

\( \hat{p} = -\frac{f_1}{f_0 \log(f_0/N)} \)

with f₀ and f₁ denoting the sample frequency at x = 0 and x = 1, respectively.

The maximum likelihood estimates are the solutions of the following two equations:

\( \bar{x} - \frac{\hat{\theta}} {1 - \hat{p}} = 0 \)

\( \bar{x} - \sum_{j=1}^{N}{\frac{f_{j}(j-1)\hat{P_{j-1}}} {N \hat{P_j}}} = 0 \)

with f_x and \( \hat{p}_{x} \) denoting the frequency at x and the Polya-Aeppli probaility mass function value at x, respectively.

You can generate estimates of theta and p based on the maximum ppcc value or the minimum chi-square goodness of fit with the commands

LET THETA1 = <value>
LET THETA2 = <value>
LET P1 = <value>
LET P2 = <value>
POLYA AEPPLI CHI-SQUARE PLOT Y
POLYA AEPPLI CHI-SQUARE PLOT Y2 X2
POLYA AEPPLI CHI-SQUARE PLOT Y3 XLOW XHIGH
POLYA AEPPLI PPCC PLOT Y
POLYA AEPPLI PPCC PLOT Y2 X2
POLYA AEPPLI PPCC PLOT Y3 XLOW XHIGH


The default values of p1 and p2 are 0.05 and 0.95, respectively. The default values of theta1 and theta2 are 1 and 25, respectively. Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the CHI-SQUARE PLOT (i.e., the minimum chi-square value) is typically preferred. However, it may sometimes be useful to perform one iteration of the PPCC PLOT to obtain a rough idea of an appropriate neighborhood for the shape parameters since the minimum chi-square statistic can generate extremely large values for non-optimal values of the shape parameter. Also, since the data is integer values, one of the binned forms is preferred for these commands.

None

None

PAPCDF	= Compute the Polya-Aeppli cumulative distribution function.
PAPPPF	= Compute the Polya-Aeppli percent point function.
LPOPDF	= Compute the Lagrange-Poisson percent point function.
BTAPDF	= Compute the Borel-Tanner probability mass function.
LOSPDF	= Compute the lost games probability mass function.
POIPDF	= Compute the Poisson probability mass function.
HERPDF	= Compute the Hermite probability mass function.
BINPDF	= Compute the binomial probability mass function.
NBPDF	= Compute the negative binomial probability mass function.
GEOPDF	= Compute the geometric probability mass function.
INTEGER FREQUENCY TABLE	= Generate a frequency table at integer values with unequal bins.
COMBINE FREQUENCY TABLE	= Convert an equal width frequency table to an unequal width frequency table.
KS PLOT	= Generate a minimum chi-square plot.
MAXIMUM LIKELIHOOD	= Perform maximum likelihood estimation for a distribution.

Douglas (1980), "Analysis with Standard Contagious Distributions", International Co-operative Publishing House, Fairland, MD.

Evans (1953), "Experimental Evidence Concerning Contagious Distributions in Ecology", Biometrika, 40, pp. 186-211.

Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 378-382.

Distributional Modeling

2006/6

 
let theta = 1.7
let lambda = 0.7
let y = polya aeppli random numbers for i = 1 1 500
.
let y3 xlow xhigh = integer frequency table y
class lower 0.5
class width 1
let amax = maximum y
let amax2 = amax + 0.5
class upper amax2
let y2 x2 = binned y
.
set write decimals 5
let k = minimum y
polya aeppli mle y
relative histogram y2 x2
limits freeze
pre-erase off
line color blue
plot pappdf(x,thetaml,pml) for x = 0 1 amax
limits
pre-erase on
line color black
let p = lambdaml
let theta = thetaml
polya aeppli chi-square goodness of fit y3 xlow xhigh
case asis
justification center
move 50 97
text Theta = ^thetaml, P = ^pml
move 50 93
text Minimum Chi-Square = ^minks, 95% CV = ^cutupp95
.
label case asis
x1label Lambda
y1label Minimum Chi-Square
let theta1 = 0.5
let theta2 = 5
let p1 = 0.1
let p2 = 0.9
polya aeppli chi-square plot y3 xlow xhigh
let theta = shape1
let p = shape2
polya aeppli chi-square goodness of fit y3 xlow xhigh
case asis
justification center
move 50 97
text Theta = ^theta, P = ^p
move 50 93
text Minimum Chi-Square = ^minks, 95% CV = ^cutupp95
    



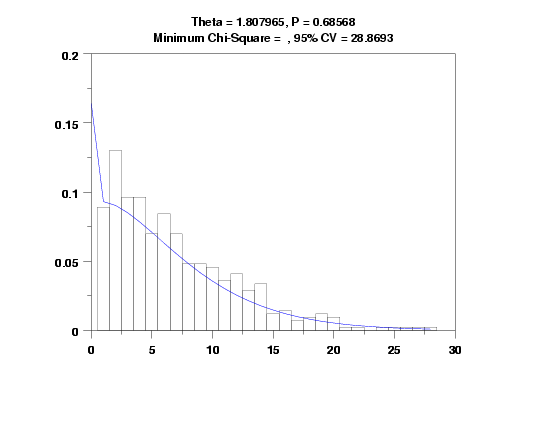
            Polya-Aeppli Parameter Estimation
 
Summary Statistics:
Number of Observations:                             500
Sample Mean:                                    5.75200
Sample Standard Deviation:                      5.38967
Sample Minimum:                                 0.00000
Sample Maximum:                                28.00000
Sample First Frequency:                        85.00000
Sample Second Frequency:                       37.00000
 
Method of Moments:
Estimate of Theta:                              1.90143
Estimate of P:                                  0.66943
 
Method of Zero Frequency and Mean:
Estimate of Theta:                              1.77196
Estimate of P:                                  0.69194
 
Method of First Two Frequencies:
Estimate of Theta:                              1.77196
Estimate of P:                                  0.24566
 
Method of Maximum Likelihood:
Estimate of Theta:                              1.80797
Estimate of P:                                  0.68568
 
 
            Chi-Square Goodness of Fit Test
 
Bin Frequency Variable:       Y3
Bin Lower Boundary Variable:  XLOW
Bin Upper Boundary Variable:  XHIGH
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: POLYA AEPPLI
Shape Parameter 1:                                 1.80797
Shape Parameter 2:                                 0.68568
 
Summary Statistics:
Total Number of Observations:                          500
Minimum Class Frequency                                  1
Number of Non-Empty Cells                               21
Degress of Freedom                                      18
Sample Minimum:                                   -0.50000
Sample Maximum:                                   28.50000
Sample Mean:                                       5.75200
Sample SD:                                         5.37741
 
Chi-Square Test Statistic Value:                  13.10322
CDF Value:                                         0.21460
P-Value                                            0.78540
 
 
 
Percent Points of the Reference Distribution
-----------------------------------
  Percent Point               Value
-----------------------------------
            0.0    =          0.000
           50.0    =         17.338
           75.0    =         21.605
           90.0    =         25.989
           95.0    =         28.869
           97.5    =         31.526
           99.0    =         34.805
           99.5    =         37.156
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%           25.989      Accept H0
     5%    95%           28.869      Accept H0
   2.5%  97.5%           31.526      Accept H0
     1%    99%           34.805      Accept H0
 
    



            Chi-Square Goodness of Fit Test
 
Bin Frequency Variable:       Y3
Bin Lower Boundary Variable:  XLOW
Bin Upper Boundary Variable:  XHIGH
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: POLYA AEPPLI
Shape Parameter 1:                                 1.81250
Shape Parameter 2:                                 0.68824
 
Summary Statistics:
Total Number of Observations:                          500
Minimum Class Frequency                                  1
Number of Non-Empty Cells                               21
Degress of Freedom                                      18
Sample Minimum:                                   -0.50000
Sample Maximum:                                   28.50000
Sample Mean:                                       5.75200
Sample SD:                                         5.37741
 
Chi-Square Test Statistic Value:                  12.87178
CDF Value:                                         0.20087
P-Value                                            0.79913
 
 
 
Percent Points of the Reference Distribution
-----------------------------------
  Percent Point               Value
-----------------------------------
            0.0    =          0.000
           50.0    =         17.338
           75.0    =         21.605
           90.0    =         25.989
           95.0    =         28.869
           97.5    =         31.526
           99.0    =         34.805
           99.5    =         37.156
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%           25.989      Accept H0
     5%    95%           28.869      Accept H0
   2.5%  97.5%           31.526      Accept H0
     1%    99%           34.805      Accept H0