HERPDF

HERPDF (LET)

Library Function

Compute the Hermite probability density function.

If X₁ and X₂ are independent Poisson random variables with shape parameters and (1/2)², respectively, then X₁ + 2X₂ follows a Hermite distribution with shape parameters and .

Some sources in the literature use the parameterization

a = a₁ =
b = a₂ = 0.5²

The shape parameters and can be expressed in terms of a₁ and a₂ as





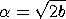
The probability mass function for the Hermite distribution is:



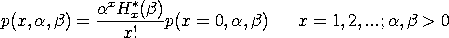
where



with denoting the modified Hermite polynomial:

with [n/2] denoting the integer part of (n/2).

The first few terms of the Hermite probability mass function are:













A general recuurence relation is:

For x < 11, Dataplot uses the above recurrence relation to compute the probabilities. For x > 10, Dataplot uses an asymptotic formula due to Patel (see Reference section below) to compute the probabilities.

LET <y> = HERPDF(<x>,<alpha>,<beta>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative integer variable, number, or parameter;
            <alpha> is a number or parameter that specifies the first shape parameter;
            <beta> is a number or parameter that specifies the second shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Hermite pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = HERPDF(3,0.5,2)
LET X2 = HERPDF(X1,ALPHA,BETA)
PLOT HERPDF(X,0.8,1.4) FOR X = 0 1 20

The following commands are available for the Hermite distribution:
LET ALPHA = <value>
LET BETA = <value>
LET Y = HERMITE RANDOM NUMBERS FOR I = 1 1 N
HERMITE PROBABILITY PLOT Y
HERMITE CHI-SQUARE GOODNESS OF FIT Y


HERMITE PPCC PLOT Y


HERMITE MAXIMUM LIKELIHOOD Y


The HERMITE MAXIMUM LIKELIHOOD command estimates the parameters of the Hermite distribution using the following methods:

1. method of moments:
   

   

   

   

   with and s² denoting the sample mean and sample variance, respectively.

   Note that this method produces an admissable estimator if s² > .

2. method of even points:
   

   

   

   

   where SE is the sum of observed frequencies at X = 0, 2, ...

   This method generates an admissable estimator only if the sum of the obserbed frequencies at even values of X is greater than the sum of the observed frequencies of the odd values of X.

3. The method of zero frequency and sample mean:
   

   

   

   

   with N0 denoting the zeroth frequency (i.e., the number of frequencies at X = 0).

   This method generates an admissable estimator only if

   

4. The method of maximum likelihood:

   The maximum likelihood estimation procedure is described in detail in Kemp and Kemp (see Reference below).

   Note that the maximum likelihood estimates can sometimes fail to converge or converge to incorrect values.

Patel discusses the various estimators for the Hermite distribution and gives some guidance on when the various estimators are most appropriate. He also gives formulas for the variances and covariances of the estimators.

None

None

HERCDF	= Compute the Hermite cumulative distribution function.
HERPPF	= Compute the Hermite percent point function.
POIPDF	= Compute the Poisson cumulative distribution function.
BINPDF	= Compute the binomial probability density function.
NBPDF	= Compute the negative binomial probability density function.
GEOPDF	= Compute the geometric probability density function.

"Discrete Univariate Distributions" Second Edition, Johnson, and Kotz, and Kemp, Wiley, 1992, pp. 357-364.

"An Asymptotic Expression for Cumulative Sum of Probabilities of the Hermite Distribution", Y. C. Patel, Communications in Statistics--Theory and Methods, 14, pp. 2233-2241.

"Some Properties of the Hermite Distribution", Kemp and Kemp, Biometrika (1965), 52, 3 and 4, P. 381.

"Even Point Estimation and Moment Estimation in Hermite Distributions", Y. C. Patel, Biometrics, 32, December, 1976, pp. 865-873.

Distributional Modeling

2004/4

 
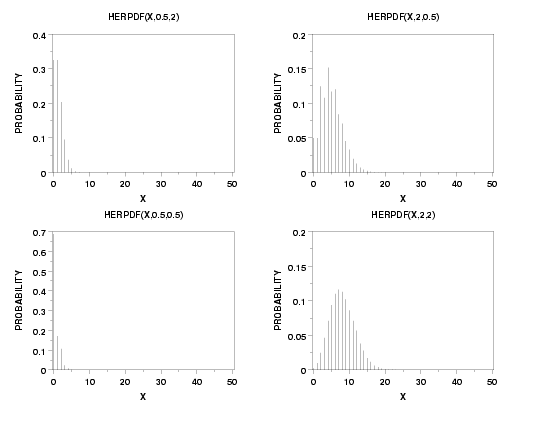
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
X1LABEL X
Y1LABEL PROBABILITY
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
TITLE SIZE 3
TITLE HERPDF(X,0.5,2)
PLOT HERPDF(X,0.5,2) FOR X = 0 1 50
TITLE HERPDF(X,2,0.5)
PLOT HERPDF(X,2,0.5) FOR X = 0 1 50
TITLE HERPDF(X,0.5,0.5)
PLOT HERPDF(X,0.5,0.5) FOR X = 0 1 50
TITLE HERPDF(X,2,2)
PLOT HERPDF(X,2,2) FOR X = 0 1 50
END OF MULTIPLOT