DIWPDF

DIWPDF (LET)

Library Function

Compute the discrete Weibull probability mass function.

The discrete Weibull distribution has the following probability mass function:

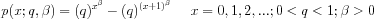
with q and denoting the shape parameters.

This distribution has application in reliability when the response of interest is a discrete variable.

LET <y> = DIWPDF(<x>,<q>,<beta>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive integer variable, number, or parameter;
            <q> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
            <beta> is a number, parameter, or variable that specifies the second shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed discrete Weibull pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DIWPDF(3,0.5,0.5)
LET Y = DIWPDF(X,0.3,0.7)
PLOT DIWPDF(X,0.6,0.4) FOR X = 1 1 20

For a number of commands utilizing the discrete Weibull distribution, it is convenient to bin the data. There are two basic ways of binning the data.
1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:
   LET AMIN = MINIMUM Y
   LET AMAX = MAXIMUM Y
   LET AMIN2 = AMIN - 0.5
   LET AMAX2 = AMAX + 0.5
   CLASS MINIMUM AMIN2
   CLASS MAXIMUM AMAX2
   CLASS WIDTH 1
   LET Y2 X2 = BINNED
   

2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands
   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
   

   If you already have equal width bins data, you can use the commands

   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
   

   The MINSIZE parameter defines the minimum class frequency. The default value is 5.

You can generate discrete Weibull random numbers, probability plots, and chi-square goodness of fit tests with the following commands:
LET N = <N>
LET Q = <value>
LET BETA = <value>
LET Y = DISCRETE WEIBULL ...
            RANDOM NUMBERS FOR I = 1 1 N


DISCRETE WEIBULL PROBABILITY PLOT Y
DISCRETE WEIBULL PROBABILITY PLOT Y2 X2
DISCRETE WEIBULL PROBABILITY PLOT ...
            Y3 XLOW XHIGH


DISCRETE WEIBULL CHI-SQUARE ...
            GOODNESS OF FIT Y
DISCRETE WEIBULL CHI-SQUARE ...
            GOODNESS OF FIT Y2 X2
DISCRETE WEIBULL CHI-SQUARE ...
            GOODNESS OF FIT Y3 XLOW XHIGH


You can generate estimates of q and based on the maximum ppcc value or the minimum chi-square goodness of fit with the commands

LET Q1 = <value>
LET Q2 = <value>
LET BETA1 = <value>
LET BETA2 = <value>
DISCRETE WEIBULL KS PLOT Y
DISCRETE WEIBULL KS PLOT Y2 X2
DISCRETE WEIBULL KS PLOT Y3 XLOW XHIGH
DISCRETE WEIBULL PPCC PLOT Y
DISCRETE WEIBULL PPCC PLOT Y2 X2
DISCRETE WEIBULL PPCC PLOT Y3 XLOW XHIGH


The default values of Q1 and Q2 are 0.05 and 0.95, respectively. The default values for beta1 and beta2 are 0.1 and 3, respectively. Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the KS PLOT (i.e., the minimum chi-square value) is typically preferred. However, it may sometimes be useful to perform one iteration of the PPCC PLOT to obtain a rough idea of an appropriate neighborhood for the shape parameters since the minimum chi-square statistic can generate extremely large values for non-optimal values of the shape parameters. Also, since the data is integer values, one of the binned forms is preferred for these commands.

None

None

DIWCDF	= Compute the discrete Weibull cumulative distribution function.
DIWCDF	= Compute the discrete Weibull hazard function.
DIWPPF	= Compute the discrete Weibull percent point function.
GLSPDF	= Compute the generalized logarithmic series probability mass function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	= Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.
POIPDF	= Compute the Poisson probability mass function.
BINPDF	= Compute the binomial probability mass function.
INTEGER FREQUENCY TABLE	= Generate a frequency table at integer values with unequal bins.
COMBINE FREQUENCY TABLE	= Convert an equal width frequency table to an unequal width frequency table.
KS PLOT	= Generate a minimum chi-square plot.
PPCC PLOT	= Generate a ppcc plot.<
PROBABILITY PLOT	= Generate a probability plot.<
MAXIMUM LIKELIHOOD	= Perform maximum likelihood estimation for a distribution.

Johnson, Kemp, and Kotz (2005), "Univariate Discrete Distributions", Third Edition, Wiley, pp. 510-511.

Nakagawa and Osaki (1975), "The Discrete Weibull Distribution", IEEE Transactions on Reliability, R-24, pp. 300-301.

Distributional Modeling

2006/8

 
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label Probability Mass
x1label X
.
ylimits 0 0.2
major ytic mark number 5
minor ytic mark number 4
xlimits 0 20
line blank
spike on
.
multiplot 2 2
.
title Q = 0.3, Beta = 0.3
plot diwpdf(x,0.3,0.3) for x = 1 1 20
.
title Q = 0.5, Beta = 0.5
plot diwpdf(x,0.5,0.5) for x = 1 1 20
.
title Q = 0.7, Beta = 0.7
plot diwpdf(x,0.7,0.7) for x = 1 1 20
.
title Q = 0.9, Beta = 0.9
plot diwpdf(x,0.9,0.9) for x = 1 1 20
.
end of multiplot
.
justification center
move 50 97
text Probability Mass Functions for Discrete Weibull
    

 
let q = 0.4
let beta = 0.5
.
let y = discrete weibull rand numbers for i = 1 1 500
.
let xmax = maximum y
let xmax2 = xmax + 0.5
let xmin = minimum y
class lower -0.5
class upper xmax2
class width 1
.
let y2 x2 = binned y
let y3 xlow xhigh = combine frequency table y2 x2
.
char blank
line solid
y1label Minimum Chi-Square
x1label Beta (curves represent values of Q)
discrete weibull ks plot y3 xlow xhigh
justification center
move 50 6
text Minimum Chi-Square = ^minks
.
let q = shape1
let beta = shape2
char x
line blank
y1label Data
x1label Theoretical
discrete weibull prob plot y2 x2
justification center
move 50 6
text PPCC = ^ppcc
.
line solid
characters blank
relative hist y2 x2
limits freeze
pre-erase off
line color blue
plot diwpdf(x,q,beta) for x = 0 1 xmax
pre-erase on
limits
.
discrete weibull chi-square goodness of fit y3 xlow xhigh
    

The following graphs and output are generated.







                   CHI-SQUARED GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            DISCRETE WEIBULL
  
 SAMPLE:
    NUMBER OF OBSERVATIONS      =      500
    NUMBER OF NON-EMPTY CELLS   =       13
    NUMBER OF PARAMETERS USED   =        2
  
 TEST:
 CHI-SQUARED TEST STATISTIC     =    7.480574
    DEGREES OF FREEDOM          =       10
    CHI-SQUARED CDF VALUE       =    0.320571
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       15.98718               ACCEPT H0
             5%       18.30704               ACCEPT H0
             1%       23.20925               ACCEPT H0