DIWCDF

DIWCDF (LET)

Library Function

Compute the discrete Weibull cumulative distribution function.

The discrete Weibull distribution has the following cumulative distribution function:

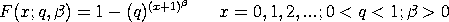
with q and denoting the shape parameters.

LET <y> = DIWCDF(<x>,<q>,<beta>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive integer variable, number, or parameter;
            <q> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
            <beta> is a number, parameter, or variable that specifies the second shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed discrete Weibull cdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DIWCDF(3,0.5,0.5)
LET Y = DIWCDF(X,0.3,0.7)
PLOT DIWCDF(X,0.6,0.4) FOR X = 1 1 20

None

None

DIWHAZ	= Compute the discrete Weibull hazard function.
DIWPDF	= Compute the discrete Weibull probability mass function.
DIWPPF	= Compute the discrete Weibull percent point function.
GLSPDF	= Compute the generalized logarithmic series probability mass function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	= Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.
POIPDF	= Compute the Poisson probability mass function.
BINPDF	= Compute the binomial probability mass function.

Johnson, Kemp, and Kotz (2005), "Univariate Discrete Distributions", Third Edition, Wiley, pp. 510-511.

Nakagawa and Osaki (1975), "The Discrete Weibull Distribution", IEEE Transactions on Reliability, R-24, pp. 300-301.

Distributional Modeling

2006/8

 
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label Probability
x1label X
.
ylimits 0 1
major ytic mark number 6
minor ytic mark number 3
xlimits 0 20
line blank
spike on
.
multiplot 2 2
.
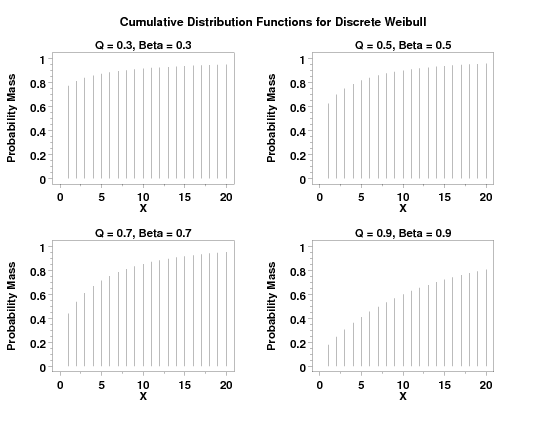
title Q = 0.3, Beta = 0.3
plot diwcdf(x,0.3,0.3) for x = 1 1 20
.
title Q = 0.5, Beta = 0.5
plot diwcdf(x,0.5,0.5) for x = 1 1 20
.
title Q = 0.7, Beta = 0.7
plot diwcdf(x,0.7,0.7) for x = 1 1 20
.
title Q = 0.9, Beta = 0.9
plot diwcdf(x,0.9,0.9) for x = 1 1 20
.
end of multiplot
.
justification center
move 50 97
text Cumulative Distribution Functions for Discrete Weibull