DIWPPF

DIWPPF (LET)

Library Function

Compute the discrete Weibull percent point function.

The discrete Weibull distribution has the following percent point function:

with q and denoting the shape parameters.

LET <y> = DIWPPF(<p>,<q>,<beta>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a positive integer variable, number, or parameter in the interval (0,1);
            <q> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
            <beta> is a number, parameter, or variable that specifies the second shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed discrete Weibull ppf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DIWPPF(0.95,0.5,0.5)
LET Y = DIWPPF(P,0.3,0.7)
PLOT DIWPPF(P,0.6,0.4) FOR P = 0 0.01 0.99

None

None

DIWCDF	= Compute the discrete Weibull cumulative distribution function.
DIWHAZ	= Compute the discrete Weibull hazard function.
DIWPDF	= Compute the discrete Weibull probability mass function.
GLSPDF	= Compute the generalized logarithmic series probability mass function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	= Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.
POIPDF	= Compute the Poisson probability mass function.
BINPDF	= Compute the binomial probability mass function.

Johnson, Kemp, and Kotz (2005), "Univariate Discrete Distributions", Third Edition, Wiley, pp. 510-511.

Nakagawa and Osaki (1975), "The Discrete Weibull Distribution", IEEE Transactions on Reliability, R-24, pp. 300-301.

Distributional Modeling

2006/8

 
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
x1label Probability
y1label X
.
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
line blank
spike on
.
multiplot 2 2
.
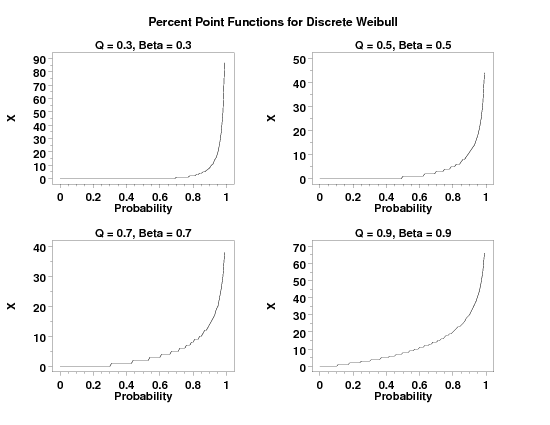
title Q = 0.3, Beta = 0.3
plot diwppf(p,0.3,0.3) for p = 0  0.01  0.99
.
title Q = 0.5, Beta = 0.5
plot diwppf(p,0.5,0.5) for p = 0  0.01  0.99
.
title Q = 0.7, Beta = 0.7
plot diwppf(p,0.7,0.7) for p = 0  0.01  0.99
.
title Q = 0.9, Beta = 0.9
plot diwppf(p,0.9,0.9) for p = 0  0.01  0.99
.
end of multiplot
.
justification center
move 50 97
text Percent Point Functions for Discrete Weibull