Next Page Previous Page Home Tools & Aids Search Handbook
5. Process Improvement
5.6. Case Studies
5.6.3. Catapult Case Study

5.6.3.3.

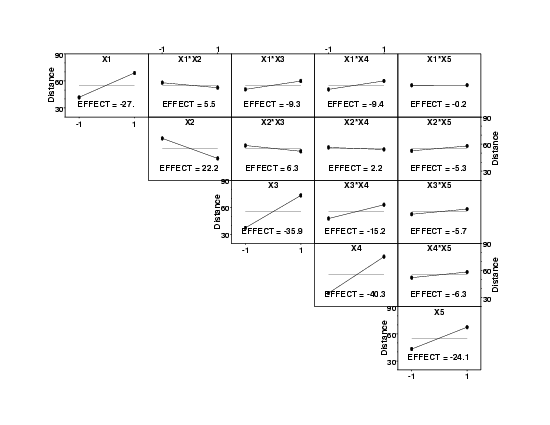
Interaction Effects
Check for Interaction Effects: Dex Mean Interaction Plot In addition to the main effects, it is also important to check for interaction effects. The dex mean interaction plot is an effective tool for viewing all 2-term interaction effects. The diagonal plots in the matrix are mean plots of each main factor. The off-diagonal plots are mean plots versus each of the C(k,2) = C(5,2) = 10 2-term interactions. All plots have the same vertical axis limits and so all are comparable. Like usual, steep lines imply a strong effects while flat lines imply no effects. The least squares estimate of the effect is given via annotation within each plot. The matrix is scanned by searching for steep lines (important factors) to flat lines (unimportant factors).

the dex mean interaction effects shows that the X3-X4 interaction is the most notable 2-term interaction

Conclusions We can make the following conclusions based on the dex interaction effects plot.
  1. Ranked List of Factors:

    1. X4 (arm length) (effect = 40.3 inches)
    2. X3 (number of bands) (effect = 35.9 inches)
    3. X1 (band height) (effect = 27.0 inches)
    4. X5 (start point) (effect = 24.0 inches)
    5. X2 (stop angle) (effect = -22.2 inches)
    6. X3*X4 interaction (effect = 15.2 inches)
    7. X1*X4 interaction (effect = 9.4 inches)
    8. X1*X3 interaction (effect = 9.3 inches)
    9. the remaining effects are not listed.

  2. Interactions: The most important interaction is X3*X4 (number of bands)*(arm length). The estimated interaction is 15.2 units, which is more than 10% of the total spread (8 to 126.5) of the data, and hence is relatively large from a simple numeric point of view. The 15.2 is to be interpreted as follows: the X3 effect changes by 15.2 units depending on whether X4 is -1 or +1. The X3 effect of 35.9 is a single number integrated over all of the data. Since the X3*x4 effect is 15.2, this implies that the X3 effect for X4 = -1 equals 35.9 - 15.2/2 = 28.3 and the X3 effect for X4 = +1 equals 35.9 + 15.2/2 = 43.5.
Limitations of Block Plots for Fractional Factorial Designs As with the full factorial designs, the block plot is a useful supplement to the dex mean plot and the dex mean interaction effects plot.

However, there are a few caveats for using block plots with fractional factorial designs.

  • Block plots are not possible in the full set of factors for fractional factorial designs. They are only possible for full factorial designs.
  • Full factorials are embedded in any 2k-p design.
  • A resolution R, 2k-p design has full factorials (possibly replicated) in any R-1 factors, i.e. R-1 balance.
  • We can generate block plots in any subset of R-1 factors.
In general, block plots are not as useful for fractional factorial designs as they are for full factorial designs. However, they are still a useful supplemental technique.

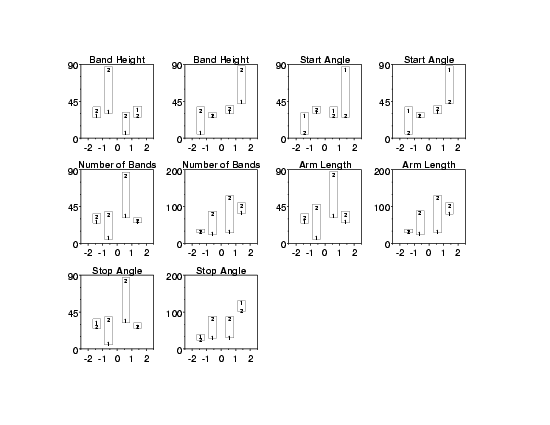
For the current design, the full set of block plots would use each factor as the primary factor, and then each combination of the remaining factors with one left out. For a 25-1 design, this would result in 5*4 = 20 block plots. As this can become overwhelming for routine use, we can often generate just a subset of these plots. For the current case, we generate two block plots for each factor (2*5=10 block plots) as the primary factor. On each of these plots, two of the remaining four factors are used as the nusciance factors.

Block Plots Plots 1 and 2 address the question: Is factor X1 important? The plot character (1 and 2) represent the 2 settings of factor 1. The horizontal axis of plot 1 is the 4 combinations of X1 and X2. The horizontal axis of plot 2 is the 4 combinations of X4 and X5. Similarly, plots 3 and 4 ask: Is factor X2 important? Plots 5 and 6 ask: Is factor X3 important? Plots 7 and 8 ask: I factor x4 important? Plots 9 and 10 ask: Is factor X5 important?

the block plots show that factors X1, X3, and X4 are statistically significant

Conclusions We can make the following conclusions based on the block plots.
  1. X1 is statistically significant. 2 is larger than 1 in 7 out of 8 cases. The probability of that (or worse) happening by chance is (8 + 1) / 256 = 3.5%.
  2. From plots 3 and 4, factor X2 has 2 > 1 in 3 out of 8 cases. This is not statistically significant.
  3. From plots 5 and 6, factor X3 has 2 > 1 in 8 out of 8 cases. This is statistically significant at the 1% level.
  4. From plots 7 and 8, factor X4 has 2 > 1 in 8 out of 8 cases. This is also statistically significant.
  5. From plots 9 and 10, factor X5 has 2 > 1 in 4 out of 8 cases. This is not statistically significant.
  6. From plots 5 and 6, the height of the vertical bar (the local factor 3 estimated effect) is large when X1*X2 = -1 and small when X1*X2 = +1 thereby implying an X3*X1*X2 interaction.
In summary, the block plot reinforces the conclusions from the dex interaction effects plot above.
Home Tools & Aids Search Handbook Previous Page Next Page