1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic

1.3.3.3.

Block Plot

Purpose:
Check to determine if a factor of interest has an effect robust over all other factors

The block plot (Filliben 1993) is an EDA tool for assessing whether the factor of interest (the primary factor) has a statistically significant effect on the response, and whether that conclusion about the primary factor effect is valid robustly over all other nuisance or secondary factors in the experiment.

It replaces the analysis of variance test with a less assumption-dependent binomial test and should be routinely used whenever we are trying to robustly decide whether a primary factor has an effect.

Sample Plot:
Weld method 2 is lower (better) than weld method 1 in 10 of 12 cases

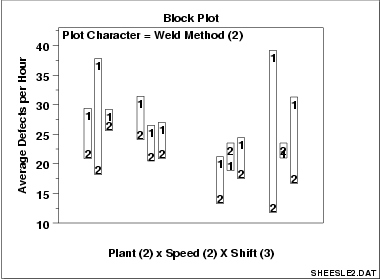
This block plot of the SHEESLE2.DAT data set reveals that in 10 of the 12 cases (bars), weld method 2 is lower (better) than weld method 1. From a binomial point of view, weld method is statistically significant.

Definition

Block Plots are formed as follows:

• Vertical axis: Response variable Y
• Horizontal axis: All combinations of all levels of all nuisance (secondary) factors X1, X2, ...
• Plot Character: Levels of the primary factor XP

Discussion:
Primary factor is denoted by plot character: within-bar plot character.

Average number of defective lead wires per hour from a study with four factors,

1. weld method (2 levels)
2. plant (2 levels)
3. speed (2 levels)
4. shift (3 levels)

are shown in the plot above. Weld method is the primary factor and the other three factors are nuisance factors. The 12 distinct positions along the horizontal axis correspond to all possible combinations of the three nuisance factors, i.e., 12 = 2 plants x 2 speeds x 3 shifts. These 12 conditions provide the framework for assessing whether any conclusions about the 2 levels of the primary factor (weld method) can truly be called "general conclusions". If we find that one weld method setting does better (smaller average defects per hour) than the other weld method setting for all or most of these 12 nuisance factor combinations, then the conclusion is in fact general and robust.

Ordering along the horizontal axis

In the above chart, the ordering along the horizontal axis is as follows:

• The left 6 bars are from plant 1 and the right 6 bars are from plant 2.
• The first 3 bars are from speed 1, the next 3 bars are from speed 2, the next 3 bars are from speed 1, and the last 3 bars are from speed 2.
• Bars 1, 4, 7, and 10 are from the first shift, bars 2, 5, 8, and 11 are from the second shift, and bars 3, 6, 9, and 12 are from the third shift.

Setting 2 is better than setting 1 in 10 out of 12 cases

In the block plot for the first bar (plant 1, speed 1, shift 1), weld method 1 yields about 28 defects per hour while weld method 2 yields about 22 defects per hour--hence the difference for this combination is about 6 defects per hour and weld method 2 is seen to be better (smaller number of defects per hour).

Is "weld method 2 is better than weld method 1" a general conclusion?

For the second bar (plant 1, speed 1, shift 2), weld method 1 is about 37 while weld method 2 is only about 18. Thus weld method 2 is again seen to be better than weld method 1. Similarly for bar 3 (plant 1, speed 1, shift 3), we see weld method 2 is smaller than weld method 1. Scanning over all of the 12 bars, we see that weld method 2 is smaller than weld method 1 in 10 of the 12 cases, which is highly suggestive of a robust weld method effect.

An event with chance probability of only 2%

What is the chance of 10 out of 12 happening by chance? This is probabilistically equivalent to testing whether a coin is fair by flipping it and getting 10 heads in 12 tosses. The chance (from the binomial distribution) of getting 10 (or more extreme: 11, 12) heads in 12 flips of a fair coin is about 2%. Such low-probability events are usually rejected as untenable and in practice we would conclude that there is a difference in weld methods.

Advantage:
Graphical and binomial

The advantages of the block plot are as follows:

• A quantitative procedure (analysis of variance) is replaced by a graphical procedure.
• An F-test (analysis of variance) is replaced with a binomial test, which requires fewer assumptions.

Questions

The block plot can provide answers to the following questions:

1. Is the factor of interest significant?
2. Does the factor of interest have an effect?
3. Does the location change between levels of the primary factor?
4. Has the process improved?
5. What is the best setting (= level) of the primary factor?
6. How much of an average improvement can we expect with this best setting of the primary factor?
7. Is there an interaction between the primary factor and one or more nuisance factors?
8. Does the effect of the primary factor change depending on the setting of some nuisance factor?
9. Are there any outliers?

Importance:
Robustly checks the significance of the factor of interest

The block plot is a graphical technique that pointedly focuses on whether or not the primary factor conclusions are in fact robustly general. This question is fundamentally different from the generic multi-factor experiment question where the analyst asks, "What factors are important and what factors are not" (a screening problem)? Global data analysis techniques, such as analysis of variance, can potentially be improved by local, focused data analysis techniques that take advantage of this difference.

Related Techniques

t test (for shift in location for exactly 2 levels)
ANOVA (for shift in location for 2 or more levels)
Bihistogram (for shift in location, variation, and distribution for exactly 2 levels).

Case Study

The block plot is demonstrated in the ceramic strength data case study.

Software

Block plots are not currently available in most general purpose statistical software programs. However they can be generated using Dataplot and, with some programming, R software.