Next Page Previous Page Home Tools & Aids Search Handbook
1. Exploratory Data Analysis
1.4. EDA Case Studies
1.4.2. Case Studies
1.4.2.3. Random Walk

1.4.2.3.2.

Test Underlying Assumptions
Goal The goal of this analysis is threefold:
  1. Determine if the univariate model:

      Y(i) = C + E(i)

    is appropriate and valid.

  2. Determine if the typical underlying assumptions for an "in control" measurement process are valid. These assumptions are:
    1. random drawings;
    2. from a fixed distribution;
    3. with the distribution having a fixed location; and
    4. the distribution having a fixed scale.

  3. Determine if the confidence interval

      YBAR +/- 2*s/SQRT(N)

    is appropriate and valid, with s denoting the standard deviation of the original data.

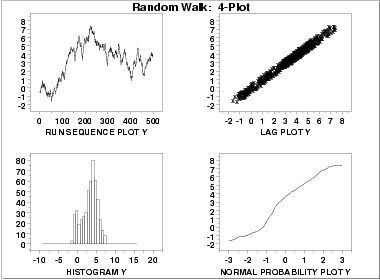
4-Plot of Data Random Walk: 4-Plot
Interpretation The assumptions are addressed by the graphics shown above:
  1. The run sequence plot (upper left) indicates significant shifts in location over time.

  2. The lag plot (upper right) indicates significant non-randomness in the data.

  3. When the assumptions of randomness and constant location and scale are not satisfied, the distributional assumptions are not meaningful. Therefore we do not attempt to make any interpretation of the histogram (lower left) or the normal probability plot (lower right).
From the above plots, we conclude that the underlying assumptions are seriously violated. Therefore the Yi = C + Ei model is not valid.

When the randomness assumption is seriously violated, a time series model may be appropriate. The lag plot often suggests a reasonable model. For example, in this case the strongly linear appearance of the lag plot suggests a model fitting Yi versus Yi-1 might be appropriate. When the data are non-random, it is helpful to supplement the lag plot with an autocorrelation plot and a spectral plot. Although in this case the lag plot is enough to suggest an appropriate model, we provide the autocorrelation and spectral plots for comparison.

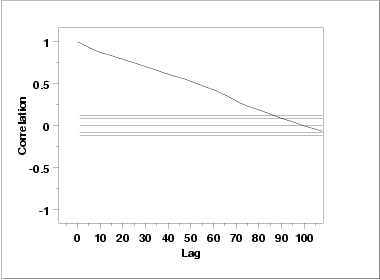
Autocorrelation Plot When the lag plot indicates significant non-randomness, it can be helpful to follow up with a an autocorrelation plot.

autocorrelation plot

This autocorrelation plot shows significant autocorrelation at lags 1 through 100 in a linearly decreasing fashion.

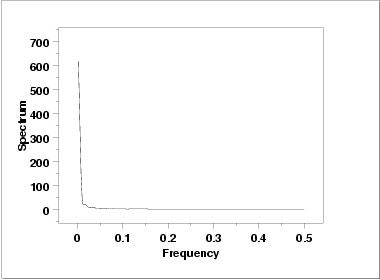
Spectral Plot Another useful plot for non-random data is the spectral plot.

spectral plot

This spectral plot shows a single dominant low frequency peak.

Quantitative Output Although the 4-plot above clearly shows the violation of the assumptions, we supplement the graphical output with some quantitative measures.
Summary Statistics As a first step in the analysis, a table of summary statistics is computed from the data. The following table, generated by Dataplot, shows a typical set of statistics. 
                                 SUMMARY
  
                      NUMBER OF OBSERVATIONS =      500
  
  
 ***********************************************************************
 *        LOCATION MEASURES         *       DISPERSION MEASURES        *
 ***********************************************************************
 *  MIDRANGE     =   0.2888407E+01  *  RANGE        =   0.9053595E+01  *
 *  MEAN         =   0.3216681E+01  *  STAND. DEV.  =   0.2078675E+01  *
 *  MIDMEAN      =   0.4791331E+01  *  AV. AB. DEV. =   0.1660585E+01  *
 *  MEDIAN       =   0.3612030E+01  *  MINIMUM      =  -0.1638390E+01  *
 *               =                  *  LOWER QUART. =   0.1747245E+01  *
 *               =                  *  LOWER HINGE  =   0.1741042E+01  *
 *               =                  *  UPPER HINGE  =   0.4682273E+01  *
 *               =                  *  UPPER QUART. =   0.4681717E+01  *
 *               =                  *  MAXIMUM      =   0.7415205E+01  *
 ***********************************************************************
 *       RANDOMNESS MEASURES        *     DISTRIBUTIONAL MEASURES      *
 ***********************************************************************
 *  AUTOCO COEF  =   0.9868608E+00  *  ST. 3RD MOM. =  -0.4448926E+00  *
 *               =   0.0000000E+00  *  ST. 4TH MOM. =   0.2397789E+01  *
 *               =   0.0000000E+00  *  ST. WILK-SHA =  -0.1279870E+02  *
 *               =                  *  UNIFORM PPCC =   0.9765666E+00  *
 *               =                  *  NORMAL  PPCC =   0.9811183E+00  *
 *               =                  *  TUK -.5 PPCC =   0.7754489E+00  *
 *               =                  *  CAUCHY  PPCC =   0.4165502E+00  *
 ***********************************************************************
The value of the autocorrelation statistic, 0.987, is evidence of a very strong autocorrelation.
Location One way to quantify a change in location over time is to fit a straight line to the data set using the index variable X = 1, 2, ..., N, with N denoting the number of observations. If there is no significant drift in the location, the slope parameter should be zero. For this data set, Dataplot generates the following output: 
 LEAST SQUARES MULTILINEAR FIT
       SAMPLE SIZE N       =      500
       NUMBER OF VARIABLES =        1
       NO REPLICATION CASE
  
  
               PARAMETER ESTIMATES           (APPROX. ST. DEV.)    T VALUE
        1  A0                   1.83351       (0.1721    )        10.65
        2  A1       X          0.552164E-02   (0.5953E-03)        9.275
  
       RESIDUAL    STANDARD DEVIATION =         1.921416
       RESIDUAL    DEGREES OF FREEDOM =         498
  
       COEF AND SD(COEF) WRITTEN OUT TO FILE DPST1F.DAT
       SD(PRED),95LOWER,95UPPER,99LOWER,99UPPER
                         WRITTEN OUT TO FILE DPST2F.DAT
       REGRESSION DIAGNOSTICS WRITTEN OUT TO FILE DPST3F.DAT
       PARAMETER VARIANCE-COVARIANCE MATRIX AND
       INVERSE OF X-TRANSPOSE X MATRIX
       WRITTEN OUT TO FILE DPST4F.DAT
The slope parameter, A1, has a t value of 9.3 which is statistically significant. This indicates that the slope cannot in fact be considered zero and so the conclusion is that we do not have constant location.
Variation One simple way to detect a change in variation is with a Bartlett test after dividing the data set into several equal-sized intervals. However, the Bartlett test is not robust for non-normality. Since we know this data set is not approximated well by the normal distribution, we use the alternative Levene test. In partiuclar, we use the Levene test based on the median rather the mean. The choice of the number of intervals is somewhat arbitrary, although values of 4 or 8 are reasonable. Dataplot generated the following output for the Levene test. 
               LEVENE F-TEST FOR SHIFT IN VARIATION
                      (ASSUMPTION: NORMALITY)
  
 1. STATISTICS
       NUMBER OF OBSERVATIONS    =      500
       NUMBER OF GROUPS          =        4
       LEVENE F TEST STATISTIC   =    10.45940
  
  
    FOR LEVENE TEST STATISTIC
       0          % POINT    =   0.0000000E+00
       50         % POINT    =   0.7897459
       75         % POINT    =    1.373753
       90         % POINT    =    2.094885
       95         % POINT    =    2.622929
       99         % POINT    =    3.821479
       99.9       % POINT    =    5.506884
  
  
          99.99989       % Point:     10.45940
  
 3. CONCLUSION (AT THE 5% LEVEL):
       THERE IS A SHIFT IN VARIATION.
       THUS: NOT HOMOGENEOUS WITH RESPECT TO VARIATION.
In this case, the Levene test indicates that the standard deviations are significantly different in the 4 intervals since the test statistic of 10.46 is greater than the 95% critical value of 2.62. Therefore we conclude that the scale is not constant.
Randomness Although the lag 1 autocorrelation coefficient above clearly shows the non-randomness, we show the output from a runs test as well. 
                    RUNS UP
  
         STATISTIC = NUMBER OF RUNS UP
             OF LENGTH EXACTLY I
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1        63.0    104.2083     10.2792       -4.01
 2        34.0     45.7167      5.2996       -2.21
 3        17.0     13.1292      3.2297        1.20
 4         4.0      2.8563      1.6351        0.70
 5         1.0      0.5037      0.7045        0.70
 6         5.0      0.0749      0.2733       18.02
 7         1.0      0.0097      0.0982       10.08
 8         1.0      0.0011      0.0331       30.15
 9         0.0      0.0001      0.0106       -0.01
10         1.0      0.0000      0.0032      311.40
  
  
         STATISTIC = NUMBER OF RUNS UP
             OF LENGTH I OR MORE
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1       127.0    166.5000      6.6546       -5.94
 2        64.0     62.2917      4.4454        0.38
 3        30.0     16.5750      3.4338        3.91
 4        13.0      3.4458      1.7786        5.37
 5         9.0      0.5895      0.7609       11.05
 6         8.0      0.0858      0.2924       27.06
 7         3.0      0.0109      0.1042       28.67
 8         2.0      0.0012      0.0349       57.21
 9         1.0      0.0001      0.0111       90.14
10         1.0      0.0000      0.0034      298.08
  
  
                   RUNS DOWN
  
         STATISTIC = NUMBER OF RUNS DOWN
             OF LENGTH EXACTLY I
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1        69.0    104.2083     10.2792       -3.43
 2        32.0     45.7167      5.2996       -2.59
 3        11.0     13.1292      3.2297       -0.66
 4         6.0      2.8563      1.6351        1.92
 5         5.0      0.5037      0.7045        6.38
 6         2.0      0.0749      0.2733        7.04
 7         2.0      0.0097      0.0982       20.26
 8         0.0      0.0011      0.0331       -0.03
 9         0.0      0.0001      0.0106       -0.01
10         0.0      0.0000      0.0032        0.00
  
  
         STATISTIC = NUMBER OF RUNS DOWN
             OF LENGTH I OR MORE
  
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1       127.0    166.5000      6.6546       -5.94
 2        58.0     62.2917      4.4454       -0.97
 3        26.0     16.5750      3.4338        2.74
 4        15.0      3.4458      1.7786        6.50
 5         9.0      0.5895      0.7609       11.05
 6         4.0      0.0858      0.2924       13.38
 7         2.0      0.0109      0.1042       19.08
 8         0.0      0.0012      0.0349       -0.03
 9         0.0      0.0001      0.0111       -0.01
10         0.0      0.0000      0.0034        0.00
  
  
         RUNS TOTAL = RUNS UP + RUNS DOWN
  
       STATISTIC = NUMBER OF RUNS TOTAL
            OF LENGTH EXACTLY I
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1       132.0    208.4167     14.5370       -5.26
 2        66.0     91.4333      7.4947       -3.39
 3        28.0     26.2583      4.5674        0.38
 4        10.0      5.7127      2.3123        1.85
 5         6.0      1.0074      0.9963        5.01
 6         7.0      0.1498      0.3866       17.72
 7         3.0      0.0193      0.1389       21.46
 8         1.0      0.0022      0.0468       21.30
 9         0.0      0.0002      0.0150       -0.01
10         1.0      0.0000      0.0045      220.19
  
  
       STATISTIC = NUMBER OF RUNS TOTAL
             OF LENGTH I OR MORE
  
 I         STAT     EXP(STAT)    SD(STAT)       Z
  
 1       254.0    333.0000      9.4110       -8.39
 2       122.0    124.5833      6.2868       -0.41
 3        56.0     33.1500      4.8561        4.71
 4        28.0      6.8917      2.5154        8.39
 5        18.0      1.1790      1.0761       15.63
 6        12.0      0.1716      0.4136       28.60
 7         5.0      0.0217      0.1474       33.77
 8         2.0      0.0024      0.0494       40.43
 9         1.0      0.0002      0.0157       63.73
10         1.0      0.0000      0.0047      210.77
  
  
        LENGTH OF THE LONGEST RUN UP         =    10
        LENGTH OF THE LONGEST RUN DOWN       =     7
        LENGTH OF THE LONGEST RUN UP OR DOWN =    10
  
        NUMBER OF POSITIVE DIFFERENCES =   258
        NUMBER OF NEGATIVE DIFFERENCES =   241
        NUMBER OF ZERO     DIFFERENCES =     0
Values in the column labeled "Z" greater than 1.96 or less than -1.96 are statistically significant at the 5% level. Numerous values in this column are much larger than +/-1.96, so we conclude that the data are not random.
Distributional Assumptions Since the quantitative tests show that the assumptions of randomness and constant location and scale are not met, the distributional measures will not be meaningful. Therefore these quantitative tests are omitted.
Home Tools & Aids Search Handbook Previous Page Next Page