1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic

1.3.3.15.

Lag Plot

Purpose: Check for randomness

A lag plot checks whether a data set or time series is random or not. Random data should not exhibit any identifiable structure in the lag plot. Non-random structure in the lag plot indicates that the underlying data are not random. Several common patterns for lag plots are shown in the examples below.

Sample Plot

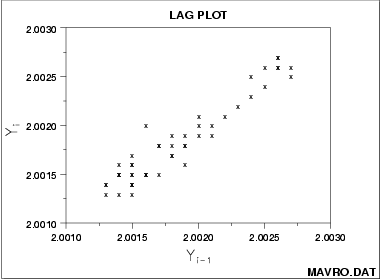
This sample lag plot of the MAVRO.DAT data set exhibits a linear pattern. This shows that the data are strongly non-random and further suggests that an autoregressive model might be appropriate.

Definition

A lag is a fixed time displacement. For example, given a data set Y₁, Y₂ ..., Y_n, Y₂ and Y₇ have lag 5 since 7 - 2 = 5. Lag plots can be generated for any arbitrary lag, although the most commonly used lag is 1.

A plot of lag 1 is a plot of the values of Y_i versus Y_i-1

• Vertical axis: Y_i for all i
• Horizontal axis: Y_i-1 for all i

Questions

Lag plots can provide answers to the following questions:

1. Are the data random?
2. Is there serial correlation in the data?
3. What is a suitable model for the data?
4. Are there outliers in the data?

Importance

Inasmuch as randomness is an underlying assumption for most statistical estimation and testing techniques, the lag plot should be a routine tool for researchers.

Examples

• Random (White Noise)
  
• Weak autocorrelation
  
• Strong autocorrelation and autoregressive model
  
• Sinusoidal model and outliers
  

Related Techniques

Autocorrelation Plot
Spectrum
Runs Test

Case Study

The lag plot is demonstrated in the beam deflection data case study.

Software

Lag plots are not directly available in most general purpose statistical software programs. Since the lag plot is essentially a scatter plot with the 2 variables properly lagged, it should be feasible to write a macro for the lag plot in most statistical programs.