1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.15. Lag Plot

1.3.3.15.3.

Lag Plot: Strong Autocorrelation and Autoregressive Model

Lag Plot

Conclusions

We can make the following conclusions based on the above plot of the random walk data set.

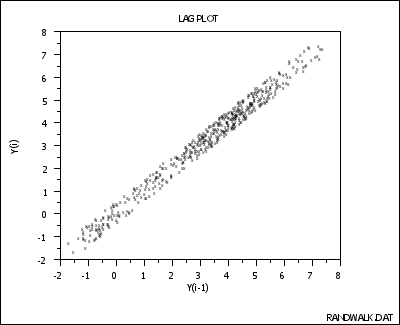
1. The data come from an underlying autoregressive model with strong positive autocorrelation
2. The data contain no outliers.

Discussion

Note the tight clustering of points along the diagonal. This is the lag plot signature of a process with strong positive autocorrelation. Such processes are highly non-random--there is strong association between an observation and a succeeding observation. In short, if you know Y_i-1 you can make a strong guess as to what Y_i will be.

If the above process were completely random, the plot would have a shotgun pattern, and knowledge of a current observation (say Y_i-1 = 3) would yield virtually no knowledge about the next observation Y_i (it could here be anywhere from -2 to +8). On the other hand, if the process had strong autocorrelation, as seen above, and if Y_i-1 = 3, then the range of possible values for Y_i is seen to be restricted to a smaller range (2 to 4)--still wide, but an improvement nonetheless (relative to -2 to +8) in predictive power.

Recommended Next Step

When the lag plot shows a strongly autoregressive pattern and only successive observations appear to be correlated, the next steps are to:

1. Extimate the parameters for the autoregressive model:
   \[ Y_{i} = A_0 + A_1*Y_{i-1} + E_{i} \]

   Since Y_i and Y_i-1 are precisely the axes of the lag plot, such estimation is a linear regression straight from the lag plot.

   The residual standard deviation for this autoregressive model will be much smaller than the residual standard deviation for the default model

   \[ Y_{i} = A_0 + E_{i} \]

2. Reexamine the system to arrive at an explanation for the strong autocorrelation. Is it due to the
   1. phenomenon under study; or
   2. drifting in the environment; or
   3. contamination from the data acquisition system?

   Sometimes the source of the problem is contamination and carry-over from the data acquisition system where the system does not have time to electronically recover before collecting the next data point. If this is the case, then consider slowing down the sampling rate to achieve randomness.