1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic

1.3.3.1.

Autocorrelation Plot

Purpose:
Check Randomness

Autocorrelation plots (Box and Jenkins, pp. 28-32) are a commonly-used tool for checking randomness in a data set. This randomness is ascertained by computing autocorrelations for data values at varying time lags. If random, such autocorrelations should be near zero for any and all time-lag separations. If non-random, then one or more of the autocorrelations will be significantly non-zero.

In addition, autocorrelation plots are used in the model identification stage for Box-Jenkins autoregressive, moving average time series models.

Autocorrelation is Only One Measure of Randomness

Note that uncorrelated does not necessarily mean random. Data that has significant autocorrelation is not random. However, data that does not show significant autocorrelation can still exhibit non-randomness in other ways. Autocorrelation is just one measure of randomness. In the context of model validation (which is the primary type of randomness we dicuss in the Handbook), checking for autocorrelation is typically a sufficient test of randomness since the residuals from a poor fitting models tend to display non-subtle randomness. However, some applications require a more rigorous determination of randomness. In these cases, a battery of tests, which might include checking for autocorrelation, are applied since data can be non-random in many different and often subtle ways.

An example of where a more rigorous check for randomness is needed would be in testing random number generators.

Sample Plot:
Autocorrelations should be near-zero for randomness. Such is not the case in this example and thus the randomness assumption fails

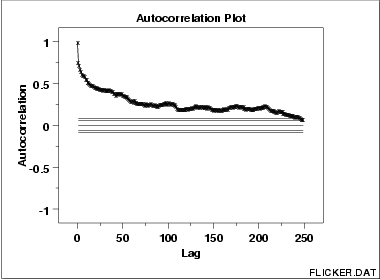
This sample autocorrelation plot of the FLICKER.DAT data set shows that the time series is not random, but rather has a high degree of autocorrelation between adjacent and near-adjacent observations.

Definition:
r(h) versus h

Autocorrelation plots are formed by

• Vertical axis: Autocorrelation coefficient
  \[ R_{h} = C_{h}/C_{0} \]

  where C_h is the autocovariance function

  \[ C_{h} = \frac{1}{N}\sum_{t=1}^{N-h}(Y_{t} - \bar{{Y}})(Y_{t+h} - \bar{{Y}}) \]

  and C₀ is the variance function

  \[ C_{0} = \frac{\sum_{t=1}^{N}(Y_{t} - \bar{Y})^2}{N} \]

  Note that R_h is between -1 and +1.

  Note that some sources may use the following formula for the autocovariance function

  \[ C_{h} = \frac{1}{N-h}\sum_{t=1}^{N-h}(Y_{t} - \bar{{Y}})(Y_{t+h} - \bar{{Y}}) \]

  Although this definition has less bias, the (1/N) formulation has some desirable statistical properties and is the form most commonly used in the statistics literature. See pages 20 and 49-50 in Chatfield for details.

• Horizontal axis: Time lag h (h = 1, 2, 3, ...)

• The above line also contains several horizontal reference lines. The middle line is at zero. The other four lines are 95 % and 99 % confidence bands. Note that there are two distinct formulas for generating the confidence bands.
  1. If the autocorrelation plot is being used to test for randomness (i.e., there is no time dependence in the data), the following formula is recommended:
     \[ \pm \frac{z_{1-\alpha/2}} {\sqrt{N}} \]

     where N is the sample size, z is the cumulative distribution function of the standard normal distribution and \( \alpha \) is the significance level. In this case, the confidence bands have fixed width that depends on the sample size. This is the formula that was used to generate the confidence bands in the above plot.

  2. Autocorrelation plots are also used in the model identification stage for fitting ARIMA models. In this case, a moving average model is assumed for the data and the following confidence bands should be generated:
     \[ \pm z_{1-\alpha/2} \sqrt{\frac{1}{N} (1 + 2 \sum_{i=1}^{k}{y_{i}^2})} \]

     where k is the lag, N is the sample size, z is the cumulative distribution function of the standard normal distribution and \( \alpha \) is the significance level. In this case, the confidence bands increase as the lag increases.

Questions

The autocorrelation plot can provide answers to the following questions:

1. Are the data random?
2. Is an observation related to an adjacent observation?
3. Is an observation related to an observation twice-removed? (etc.)
4. Is the observed time series white noise?
5. Is the observed time series sinusoidal?
6. Is the observed time series autoregressive?
7. What is an appropriate model for the observed time series?
8. Is the model
   Y = constant + error

   valid and sufficient?

9. Is the formula \[ s_{\bar{{Y}}} = s/\sqrt{N} \] valid?

Importance:
Ensure validity of engineering conclusions

Randomness (along with fixed model, fixed variation, and fixed distribution) is one of the four assumptions that typically underlie all measurement processes. The randomness assumption is critically important for the following three reasons:

1. Most standard statistical tests depend on randomness. The validity of the test conclusions is directly linked to the validity of the randomness assumption.

2. Many commonly-used statistical formulae depend on the randomness assumption, the most common formula being the formula for determining the standard deviation of the sample mean:
   \[ s_{\bar{{Y}}} = s/\sqrt{N} \]

   where s is the standard deviation of the data. Although heavily used, the results from using this formula are of no value unless the randomness assumption holds.

3. For univariate data, the default model is
   Y = constant + error

   If the data are not random, this model is incorrect and invalid, and the estimates for the parameters (such as the constant) become nonsensical and invalid.

In short, if the analyst does not check for randomness, then the validity of many of the statistical conclusions becomes suspect. The autocorrelation plot is an excellent way of checking for such randomness.

Examples

Examples of the autocorrelation plot for several common situations are given in the following pages.

1. Random (= White Noise)
   
2. Weak autocorrelation
   
3. Strong autocorrelation and autoregressive model
   
4. Sinusoidal model
   

Related Techniques

Partial Autocorrelation Plot
Lag Plot
Spectral Plot
Seasonal Subseries Plot

Case Study

The autocorrelation plot is demonstrated in the beam deflection data case study.

Software

Autocorrelation plots are available in most general purpose statistical software programs.