1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.32. 4-Plot
Check Underlying Statistical Assumptions
Although the 4-plot has an obvious use for univariate and time series data, its usefulness extends far beyond that. Many statistical models of the form
-
\[ Y_{i} = f(X_{1}, ... , X_{k}) + E_{i} \]
Process Has Fixed Location, Fixed Variation, Non-Random (Oscillatory), Non-Normal U-Shaped Distribution, and Has 3 Outliers.
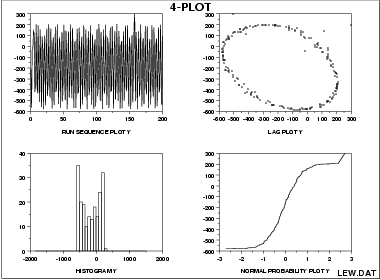
This 4-plot of the LEW.DAT data set reveals the following:
- the fixed location assumption is justified as shown by the run sequence plot in the upper left corner.
- the fixed variation assumption is justified as shown by the run sequence plot in the upper left corner.
- the randomness assumption is violated as shown by the non-random (oscillatory) lag plot in the upper right corner.
- the assumption of a common, normal distribution is violated as shown by the histogram in the lower left corner and the normal probability plot in the lower right corner. The distribution is non-normal and is a U-shaped distribution.
- there are several outliers apparent in the lag plot in the upper right corner.
1. Run Sequence Plot;
2. Lag Plot;
3. Histogram;
4. Normal Probability Plot
- Run sequence plot to test fixed location and variation.
- Vertically: Yi
- Horizontally: i
- Lag Plot to test randomness.
- Vertically: Yi
- Horizontally: Yi-1
- Histogram to test (normal) distribution.
- Vertically: Counts
- Horizontally: Y
- Normal probability plot to test normal distribution.
- Vertically: Ordered Yi
- Horizontally: Theoretical values from a normal N(0,1) distribution for ordered Yi
- Is the process in-control, stable, and predictable?
- Is the process drifting with respect to location?
- Is the process drifting with respect to variation?
- Are the data random?
- Is an observation related to an adjacent observation?
- If the data are a time series, is white noise?
- If the data are a time series and not white noise, is it sinusoidal, autoregressive, etc.?
- If the data are non-random, what is a better model?
- Does the process follow a normal distribution?
- If non-normal, what distribution does the process follow?
- Is the model
-
\[ Y_{i} = A_0 + E_{i} \]
valid and sufficient?
- If the default model is insufficient, what is a better model?
- Is the formula \[ s_{\bar{Y}} = s/\sqrt{N} \] valid?
- Is the sample mean a good estimator of the process location?
- If not, what would be a better estimator?
- Are there any outliers?
Testing Underlying Assumptions Helps Ensure the Validity of the Final Scientific and Engineering Conclusions
- random drawings;
- from a fixed distribution;
- with that distribution having a fixed location; and
- with that distribution having fixed variation.
Inasmuch as the validity of the final scientific and engineering conclusions is inextricably linked to the validity of these same 4 underlying assumptions, it naturally follows that there is a real necessity for all 4 assumptions to be routinely tested. The 4-plot (run sequence plot, lag plot, histogram, and normal probability plot) is seen as a simple, efficient, and powerful way of carrying out this routine checking.
Flat, Equi-Banded, Random, Bell-Shaped, and Linear
- If the fixed location assumption holds, then the run sequence plot will be flat and non-drifting.
- If the fixed variation assumption holds, then the vertical spread in the run sequence plot will be approximately the same over the entire horizontal axis.
- If the randomness assumption holds, then the lag plot will be structureless and random.
- If the fixed distribution assumption holds (in particular, if the fixed normal distribution assumption holds), then the histogram will be bell-shaped and the normal probability plot will be approximatelylinear.
Lag Plot
Histogram
Normal Probability Plot
Autocorrelation Plot
Spectral Plot
PPCC Plot

