1.3.5.17.1. Grubbs' Test for Outliers

1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.5. Quantitative Techniques
1.3.5.17. Detection of Outliers

1.3.5.17.1. Grubbs' Test for Outliers

Purpose:
Detection of Outliers

Grubbs' test (Grubbs 1969 and Stefansky 1972) is used to detect a single outlier in a univariate data set that follows an approximately normal distribution.

If you suspect more than one outlier may be present, it is recommended that you use either the Tietjen-Moore test or the generalized extreme studentized deviate test instead of the Grubbs' test.

Grubbs' test is also known as the maximum normed residual test.

Definition

Grubbs' test is defined for the hypothesis:

H₀:	There are no outliers in the data set
H_a:	There is exactly one outlier in the data set
Test Statistic:	The Grubbs' test statistic is defined as: \( G = \frac{\max{\|Y_{i} - \bar{Y}\|}} {s} \) with \(\bar{Y}\) and s denoting the sample mean and standard deviation, respectively. The Grubbs' test statistic is the largest absolute deviation from the sample mean in units of the sample standard deviation. This is the two-sided version of the test. The Grubbs' test can also be defined as one of the following one-sided tests: test whether the minimum value is an outlier \( G = \frac{\bar{Y} - Y_{min}} {s} \) with Y_min denoting the minimum value. test whether the maximum value is an outlier \( G = \frac{Y_{max} - \bar{Y}} {s} \) with Y_max denoting the maximum value.
Significance Level:	α
Critical Region:	For the two-sided test, the hypothesis of no outliers is rejected if \( G > \frac{(N-1)} {\sqrt{N}} \sqrt{\frac{(t_{\alpha/(2N),N-2})^2} {N-2+(t_{\alpha/(2N),N-2})^2}} \) with \(t_{\alpha/(2N),N-2}\) denoting the critical value of the t distribution with (N-2) degrees of freedom and a significance level of α/(2N). For one-sided tests, we use a significance level of level of α/N.

Grubbs' Test Example

The Tietjen and Moore paper gives the following set of 8 mass spectrometer measurements on a uranium isotope:

199.31 199.53 200.19 200.82 201.92 201.95 202.18 245.57 As a first step, a normal probability plot was generated

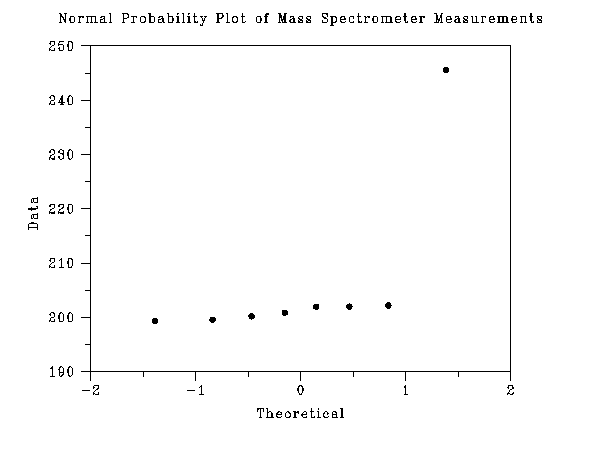
This plot indicates that the normality assumption is reasonable with the exception of the maximum value. We therefore compute Grubbs' test for the case that the maximum value, 245.57, is an outlier.

      H₀:  there are no outliers in the data
      H_a:  the maximum value is an outlier

      Test statistic:  G = 2.4687 
      Significance level:  α = 0.05
      Critical value for an upper one-tailed test:  2.032          
      Critical region:  Reject H₀ if G > 2.032

For this data set, we reject the null hypothesis and conclude that the maximum value is in fact an outlier at the 0.05 significance level.

Questions

Grubbs' test can be used to answer the following questions:

Is the maximum value an outlier?
Is the minimum value an outlier?

Importance

Many statistical techniques are sensitive to the presence of outliers. For example, simple calculations of the mean and standard deviation may be distorted by a single grossly inaccurate data point.

Checking for outliers should be a routine part of any data analysis. Potential outliers should be examined to see if they are possibly erroneous. If the data point is in error, it should be corrected if possible and deleted if it is not possible. If there is no reason to believe that the outlying point is in error, it should not be deleted without careful consideration. However, the use of more robust techniques may be warranted. Robust techniques will often downweight the effect of outlying points without deleting them.

Related Techniques

Several graphical techniques can, and should, be used to help detect outliers. A simple normal probability plot, run sequence plot, a box plot, or a histogram should show any obviously outlying points. In addition to showing potential outliers, several of these graphics also help assess whether the data follow an approximately normal distribution.

Normal Probability Plot

Case Study

Heat flow meter data.

Software

Some general purpose statistical software programs support the Grubbs' test. Both Dataplot code and R code can be used to generate the analyses in this section.