1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic

1.3.3.21.

Normal Probability Plot

Purpose:
Check If Data Are Approximately Normally Distributed

The normal probability plot (Chambers et al., 1983) is a graphical technique for assessing whether or not a data set is approximately normally distributed.

The data are plotted against a theoretical normal distribution in such a way that the points should form an approximate straight line. Departures from this straight line indicate departures from normality.

The normal probability plot is a special case of the probability plot. We cover the normal probability plot separately due to its importance in many applications.

Sample Plot

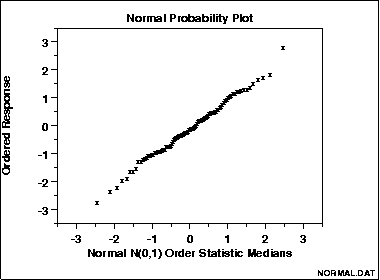
The points on this normal probablity plot of 100 normal random numbers form a nearly linear pattern, which indicates that the normal distribution is a good model for this data set.

Definition:
Ordered Response Values Versus Normal Order Statistic Medians

The normal probability plot is formed by:

• Vertical axis: Ordered response values
• Horizontal axis: Normal order statistic medians

The observations are plotted as a function of the corresponding normal order statistic medians which are defined as:

N_i = G(U_i)

where U_i are the uniform order statistic medians (defined below) and G is the percent point function of the normal distribution. The percent point function is the inverse of the cumulative distribution function (probability that x is less than or equal to some value). That is, given a probability, we want the corresponding x of the cumulative distribution function.

The uniform order statistic medians (see Filliben 1975) can be approximated by:

U_i = 1 - U_n    for i = 1
U_i = (i - 0.3175)/(n + 0.365)    for i = 2, 3, ..., n-1
U_i = 0.5^(1/n)    for i = n

In addition, a straight line can be fit to the points and added as a reference line. The further the points vary from this line, the greater the indication of departures from normality.

Probability plots for distributions other than the normal are computed in exactly the same way. The normal percent point function (the G) is simply replaced by the percent point function of the desired distribution. That is, a probability plot can easily be generated for any distribution for which you have the percent point function.

One advantage of this method of computing probability plots is that the intercept and slope estimates of the fitted line are in fact estimates for the location and scale parameters of the distribution. Although this is not too important for the normal distribution since the location and scale are estimated by the mean and standard deviation, respectively, it can be useful for many other distributions.

The correlation coefficient of the points on the normal probability plot can be compared to a table of critical values to provide a formal test of the hypothesis that the data come from a normal distribution.

Questions

The normal probability plot is used to answer the following questions.

1. Are the data normally distributed?
2. What is the nature of the departure from normality (data skewed, shorter than expected tails, longer than expected tails)?

Importance:
Check Normality Assumption

The underlying assumptions for a measurement process are that the data should behave like:

1. random drawings;
2. from a fixed distribution;
3. with fixed location;
4. with fixed scale.

Probability plots are used to assess the assumption of a fixed distribution. In particular, most statistical models are of the form:

response = deterministic + random

where the deterministic part is the fit and the random part is error. This error component in most common statistical models is specifically assumed to be normally distributed with fixed location and scale. This is the most frequent application of normal probability plots. That is, a model is fit and a normal probability plot is generated for the residuals from the fitted model. If the residuals from the fitted model are not normally distributed, then one of the major assumptions of the model has been violated.

Examples

1. Data are normally distributed
2. Data have short tails
3. Data have fat tails
4. Data are skewed right

Related Techniques

Histogram
Probability plots for other distributions (e.g., Weibull)
Probability plot correlation coefficient plot (PPCC plot) Anderson-Darling Goodness-of-Fit Test
Chi-Square Goodness-of-Fit Test
Kolmogorov-Smirnov Goodness-of-Fit Test

Case Study

The normal probability plot is demonstrated in the heat flow meter data case study.

Software

Most general purpose statistical software programs can generate a normal probability plot.