1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.5. Quantitative Techniques

1.3.5.16.

Kolmogorov-Smirnov Goodness-of-Fit Test

Purpose:
Test for Distributional Adequacy

The Kolmogorov-Smirnov test (Chakravart, Laha, and Roy, 1967) is used to decide if a sample comes from a population with a specific distribution.

The Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N ordered data points Y₁, Y₂, ..., Y_N, the ECDF is defined as

\[ E_{N} = n(i)/N \]

where n(i) is the number of points less than Y_i and the Y_i are ordered from smallest to largest value. This is a step function that increases by 1/N at the value of each ordered data point.

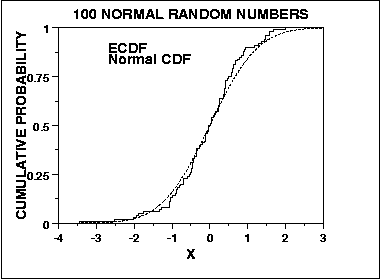
The graph below is a plot of the empirical distribution function with a normal cumulative distribution function for 100 normal random numbers. The K-S test is based on the maximum distance between these two curves.

Characteristics and Limitations of the K-S Test

An attractive feature of this test is that the distribution of the K-S test statistic itself does not depend on the underlying cumulative distribution function being tested. Another advantage is that it is an exact test (the chi-square goodness-of-fit test depends on an adequate sample size for the approximations to be valid). Despite these advantages, the K-S test has several important limitations:

1. It only applies to continuous distributions.
2. It tends to be more sensitive near the center of the distribution than at the tails.
3. Perhaps the most serious limitation is that the distribution must be fully specified. That is, if location, scale, and shape parameters are estimated from the data, the critical region of the K-S test is no longer valid. It typically must be determined by simulation.

Several goodness-of-fit tests, such as the Anderson-Darling test and the Cramer Von-Mises test, are refinements of the K-S test. As these refined tests are generally considered to be more powerful than the original K-S test, many analysts prefer them. Also, the advantage for the K-S test of having the critical values be indpendendent of the underlying distribution is not as much of an advantage as first appears. This is due to limitation 3 above (i.e., the distribution parameters are typically not known and have to be estimated from the data). So in practice, the critical values for the K-S test have to be determined by simulation just as for the Anderson-Darling and Cramer Von-Mises (and related) tests.

Note that although the K-S test is typically developed in the context of continuous distributions for uncensored and ungrouped data, the test has in fact been extended to discrete distributions and to censored and grouped data. We do not discuss those cases here.

Definition

The Kolmogorov-Smirnov test is defined by:

H0:	The data follow a specified distribution
Ha:	The data do not follow the specified distribution
Test Statistic:	The Kolmogorov-Smirnov test statistic is defined as \[ D = \max_{1 \le i \le N} \left( F(Y_{i}) - \frac{i-1} {N}, \frac{i}{N} - F(Y_{i}) \right) \] where F is the theoretical cumulative distribution of the distribution being tested which must be a continuous distribution (i.e., no discrete distributions such as the binomial or Poisson), and it must be fully specified (i.e., the location, scale, and shape parameters cannot be estimated from the data).
Significance Level:	α
Critical Values:	The hypothesis regarding the distributional form is rejected if the test statistic, D, is greater than the critical value obtained from a table. There are several variations of these tables in the literature that use somewhat different scalings for the K-S test statistic and critical regions. These alternative formulations should be equivalent, but it is necessary to ensure that the test statistic is calculated in a way that is consistent with how the critical values were tabulated. We do not provide the K-S tables in the Handbook since software programs that perform a K-S test will provide the relevant critical values.

Technical Note

Previous editions of e-Handbook gave the following formula for the computation of the Kolmogorov-Smirnov goodness of fit statistic:

\[ D = \max_{1 \le i \le N} \left| F(Y_{i}) - \frac{i} {N} \right| \]

This formula is in fact not correct. Note that this formula can be rewritten as:

\[ D = \max_{1 \le i \le N} (F(Y_{i}) - \frac{i} {N}, \frac{i}{N} - F(Y_{i})) \]

This form makes it clear that an upper bound on the difference between these two formulas is i/N. For actual data, the difference is likely to be less than the upper bound.

For example, for N = 20, the upper bound on the difference between these two formulas is 0.05 (for comparison, the 5% critical value is 0.294). For N = 100, the upper bound is 0.001. In practice, if you have moderate to large sample sizes (say N ≥ 50), these formulas are essentially equivalent.

Kolmogorov-Smirnov Test Example

We generated 1,000 random numbers for normal, double exponential, t with 3 degrees of freedom, and lognormal distributions. In all cases, the Kolmogorov-Smirnov test was applied to test for a normal distribution.

The normal random numbers were stored in the variable Y1, the double exponential random numbers were stored in the variable Y2, the t random numbers were stored in the variable Y3, and the lognormal random numbers were stored in the variable Y4.

      H0:  the data are normally distributed
      Ha:  the data are not normally distributed

      Y1 test statistic:  D = 0.0241492  
      Y2 test statistic:  D = 0.0514086 
      Y3 test statistic:  D = 0.0611935
      Y4 test statistic:  D = 0.5354889

      Significance level:  α = 0.05
      Critical value:  0.04301    
      Critical region:  Reject H0 if D > 0.04301
      

As expected, the null hypothesis is not rejected for the normally distributed data, but is rejected for the remaining three data sets that are not normally distributed.

Questions

The Kolmogorov-Smirnov test can be used to answer the following types of questions:

• Are the data from a normal distribution?
• Are the data from a log-normal distribution?
• Are the data from a Weibull distribution?
• Are the data from an exponential distribution?
• Are the data from a logistic distribution?

Importance

Many statistical tests and procedures are based on specific distributional assumptions. The assumption of normality is particularly common in classical statistical tests. Much reliability modeling is based on the assumption that the data follow a Weibull distribution.

There are many non-parametric and robust techniques that are not based on strong distributional assumptions. By non-parametric, we mean a technique, such as the sign test, that is not based on a specific distributional assumption. By robust, we mean a statistical technique that performs well under a wide range of distributional assumptions. However, techniques based on specific distributional assumptions are in general more powerful than these non-parametric and robust techniques. By power, we mean the ability to detect a difference when that difference actually exists. Therefore, if the distributional assumptions can be confirmed, the parametric techniques are generally preferred.

If you are using a technique that makes a normality (or some other type of distributional) assumption, it is important to confirm that this assumption is in fact justified. If it is, the more powerful parametric techniques can be used. If the distributional assumption is not justified, using a non-parametric or robust technique may be required.

Related Techniques

Anderson-Darling goodness-of-fit Test
Chi-Square goodness-of-fit Test
Shapiro-Wilk Normality Test
Probability Plots
Probability Plot Correlation Coefficient Plot

Software

Some general purpose statistical software programs support the Kolmogorov-Smirnov goodness-of-fit test, at least for the more common distributions. Both Dataplot code and R code can be used to generate the analyses in this section.