

|
UTSPDFName:
![f(x,a,b,d,n1,n3,alpha) = [alpha*n1*n3/(alpha*(b-a)*n3+(d-b)*n1)]
*((x-a)/(b-a))**(n1-1) a <= x < b;
= [n1*n3/(alpha*(b-a)*n3+(d-b)*n1)]*((d-x)/(d-b))**(n3-1)
b <= x < d;
= 0 x < a, x >= d](eqns/utspdfg.gif)
where
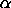 > 0 > 0
The parameters a and d are lower and upper limit
parameters. The b parameter is a threshold parameter
(the distribution has a discontinuity at this point). The
The case where a = 0 and d = 1 is referred to as the standard uneven two-sided power distribution. The a and d parameters are lower and upper limit parameters. These are related to location and scale parameters as follows
scale = d - a Kotz and Van Dorp show that the standard uneven two-sided power distribution can also be given as
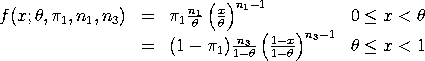
where
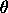 = b = b
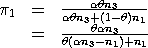
0 ≤  ≤ 1
≤ 1
Kotz and Van Dorp use this form to derive some of the properties of this distribution.
The unveven two-sided power distribution is a generalization of the
two-sided power distribution. It is also
related to the (the center part of the generalized trapezoid
distribution shrinks to a single point). See Van Dorp and Kotz for
details.
The special case where
<SUBSET/EXCEPT/FOR qualification> where <x> is a variable, number, or parameter containing values in the interval (a,d); <a> is a number, parameter, or variable that specifies the first shape parameter; <b> is a number, parameter, or variable that specifies the second shape parameter; <d> is a number, parameter, or variable that specifies the third shape parameter; <n1> is a number, parameter, or variable that specifies the fourth shape parameter; <n3> is a number, parameter, or variable that specifies the fifth shape parameter; <alpha> is a number, parameter, or variable that specifies the sixth shape parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed pdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET Y = UTSPDF(X,0,0.8,1,2,2,0.5) LET Y = UTSPDF(X,A,B,D,N1,N3,ALPHA)
LET B = <value> LET D = <value> LET N1 = <value> LET N3 = <value> LET ALPHA = <value> LET Y = UNEVEN TWO-SIDED POWER RANDOM NUMBERS ... FOR I = 1 1 N UNEVEN TWO-SIDED POWER PROBABILITY PLOT Y UNEVEN TWO-SIDED POWER PROBABILITY PLOT Y2 X2 UNEVEN TWO-SIDED POWER PROBABILITY PLOT Y3 XLOW XHIGH UNEVEN TWO-SIDED POWER KOLMOGOROV SMIRNOV ... GOODNESS OF FIT Y UNEVEN TWO-SIDED POWER CHI-SQUARE ... GOODNESS OF FIT Y2 X2 UNEVEN TWO-SIDED POWER CHI-SQUARE ... GOODNESS OF FIT Y3 XLOW XHIGH Note that
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
MULTIPLOT 2 2
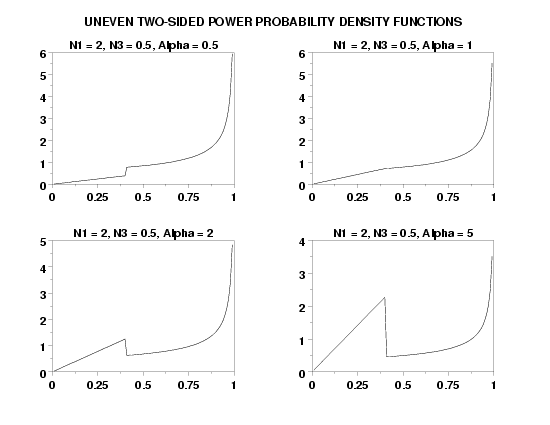
LET A = 0
LET B = 0.4
LET D = 1.0
LET N1 = 2
LET N3 = 0.5
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Probability Density Functions
.
MULTIPLOT 2 2
LET N1 = 0.5
LET N3 = 2
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A 0.01 D
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Probability Density Functions
.
MULTIPLOT 2 2
LET N1 = 2
LET N3 = 2
LET A2 = 0.01
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSPDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Probability Density Functions
Date created: 12/17/2007 |