

|
UTSCDFName:
![F(x,a,b,d,n1,n3,alpha) = 0 x < a;
= [alpha*(b-a)*n3/(alpha*(b-a)*n3+(d-b)*n1)]*((x-a)/(b-a))^n1
a <= x < b;
= 1 - [(d-b)*n1/(alpha*(b-a)*n3+(d-b)*n1)]*((d-x)/(d-b))^n3
b <= x < d;
= 1
x >= d](eqns/utscdfg.gif)
where
n1, n3,  > 0 > 0
The case where a = 0 and d = 1 is referred to as the standard uneven two-sided power distribution. The a and d parameters are lower and upper limit parameters. These are related to location and scale parameters as follows
scale = d - a Kotz and Van Dorp show that the standard uneven two-sided power cumulative distribution can also be given as
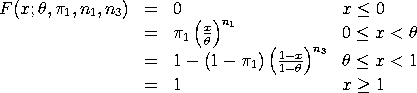
where
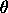 = b = b
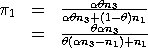
0 ≤ 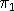 ≤ 1
≤ 1
Kotz and Van Dorp use this form to derive some of the properties of this distribution.
The unveven two-sided power distribution is a generalization of the
two-sided power distribution. It is also
related to the (the center part of the generalized trapezoid
distribution shrinks to a single point). See Van Dorp and Kotz for
details.
The special case where
<SUBSET/EXCEPT/FOR qualification> where <x> is a variable, number, or parameter containing values in the interval (a,d); <a> is a number, parameter, or variable that specifies the first shape parameter; <b> is a number, parameter, or variable that specifies the second shape parameter; <d> is a number, parameter, or variable that specifies the third shape parameter; <n1> is a number, parameter, or variable that specifies the fourth shape parameter; <n3> is a number, parameter, or variable that specifies the fifth shape parameter; <alpha> is a number, parameter, or variable that specifies the sixth shape parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed cdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET Y = UTSCDF(X,0,0.8,1,2,2,0.5) LET Y = UTSCDF(X,A,B,D,N1,N3,ALPHA)
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
MULTIPLOT 2 2
LET A = 0
LET B = 0.4
LET D = 1.0
LET N1 = 2
LET N3 = 0.5
LET A2 = A + 0.01
LET D2 = D - 0.01
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Cumulative Distribution Functions
.
MULTIPLOT 2 2
LET N1 = 0.5
LET N3 = 2
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Cumulative Distribution Functions
.
MULTIPLOT 2 2
LET N1 = 2
LET N3 = 2
.
LET ALPHA = 0.5
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 1.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 2.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
LET ALPHA = 5.0
TITLE N1 = ^n1, N3 = ^n3, Alpha = ^alpha
PLOT UTSCDF(X,A,B,D,N1,N3,ALPHA) FOR X = A2 0.01 D2
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Uneven Two-Sided Power Cumulative Distribution Functions
Date created: 12/17/2007 |