TOPPPF

TOPPPF (LET)

Library Function

Compute the Topp and Leone percent point function with shape parameter .

The standard Topp and Leone distribution has the following percent point function:

with denoting the shape parameter.

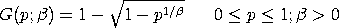
This distribution can be extended with lower and upper bound parameters. If a and b denote the lower and upper bounds, respectively, then the location and scale parameters are:

location = a
scale = b - a

The general form of the distribution can then be found by using the relation

LET <y> = TOPPPF(<p>,<beta>,<a>,<b>)
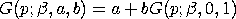
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable containing values in the interval (0,1);
            <y> is a variable or a parameter (depending on what <p> is) where the computed Topp and Leone ppf value is stored;
            <beta> is a positive number, parameter, or variable that specifies the shape parameter;
            <a> is a number, parameter, or variable that specifies the lower limit;
            <b> is a number, parameter, or variable that specifies the upper limit;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If a and b are omitted, they default to 0 and 1, respectively.

LET A = TOPPPF(0.3,0.2)
LET Y = TOPPPF(P,0.5,0,5)
PLOT TOPPPF(P,2,0,3) FOR P = 0 0.01 1

None

None

TOPCDF	= Compute the Topp and Leone cumulative distribution function.
TOPPDF	= Compute the Topp and Leone probability density function.
RGTPDF	= Compute the generalized reflected Topp and Leone probability density function.
GTLPDF	= Compute the generalized Topp and Leone probability density function.
TSPPDF	= Compute the two-sided power probability density function.
BETPDF	= Compute the beta probability density function.
TRIPDF	= Compute the triangular probability density function.
TRAPDF	= Compute the trapezoid probability density function.
UNIPDF	= Compute the uniform probability density function.
POWPDF	= Compute the power probability density function.
JSBPDF	= Compute the Johnson SB probability density function.

Samuel Kotz and J. Rene Van Dorp 2004, "Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications", World Scientific, chapter 2.

Distributional Modeling

2007/2

LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR
.
LET BETA  = 0.5
TITLE Beta = ^beta
PLOT TOPPPF(P,BETA) FOR P = 0  0.01  1
.
LET BETA  = 1
TITLE Beta = ^beta
PLOT TOPPPF(P,BETA) FOR P = 0  0.01  1
.
LET BETA  = 1.5
TITLE Beta = ^beta
PLOT TOPPPF(P,BETA) FOR P = 0  0.01  1
.
LET BETA  = 2
TITLE Beta = ^beta
PLOT TOPPPF(P,BETA) FOR P = 0  0.01  1
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT TOPP AND LEONE PPF FUNCTIONS