FALSE POSITIVES

FALSE POSITIVES (LET)

Let Subcommand

Compute the proportion of false positives between two binary variables.

Given two variables with n parired observations where each variable has exactly two possible outcomes, we can generate the following 2x2 table:

	Variable 2
Variable 1	Success	Failure	Row Total
Success	N11	N12	N11 + N12
Failure	N21	N22	N21 + N22
Column Total	N11 + N21	N12 + N22	N

The parameters N₁₁, N₁₂, N₂₁, and N₂₂ denote the counts for each category.

Success and failure can denote any binary response. Dataplot expects "success" to be coded as "1" and "failure" to be coded as "0". Some typical examples would be:

1. Variable 1 denotes whether or not a patient has a disease (1 denotes disease is present, 0 denotes disease not present). Variable 2 denotes the result of a test to detect the disease (1 denotes a positive result and 0 denotes a negative result).

2. Variable 1 denotes whether an object is present or not (1 denotes present, 0 denotes absent). Variable 2 denotes a detection device (1 denotes object detected and 0 denotes object not detected).

In these examples, the "ground truth" is typically given as variable 1 while some estimator of the ground truth is given as variable 2.

The proportion of false positives is then N₂₁/N (i.e., the number of cases where variable 1 is a failure and variable 2 is a success). In the context of the first examples above, the test detected the disease when it was in fact not present.

LET <par> = FALSE POSITIVE <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed false positive proportion is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = FALSE POSITIVE Y1 Y2
LET A = FALSE POSITIVE Y1 Y2 SUBSET TAG > 2

The two variables must have the same number of elements.

There are two ways you can define the response variables:
1. Raw data - in this case, the variables contain 0's and 1's.

   If the data is not coded as 0's and 1's, Dataplot will check for the number of distinct values. If there are two distinct values, the minimum value is converted to 0's and the maximum value is converted to 1's. If there is a single distinct value, it is converted to 0's if it is less than 0.5 and to 1's if it is greater than or equal to 0.5. If there are more than two distinct values, an error is returned.

2. Summary data - if there are two observations, the data is assummed to be the 2x2 summary table. That is,
   Y1(1) = N11
   Y1(2) = N21
   Y2(1) = N12
   Y2(2) = N22
   

This commands returns the proportion of false positives. If you need raw counts or percentages, you can enter the commands
LET N = SIZE Y1
LET FALSEPOS = FALSE POSITIVE Y1 Y2
LET FPCOUNT = N*FALSEPOS
LET FPPERC = 100*FALSEPOS

This command has been extended to support the case for RxC tables where R denotes the number of categories for variable one and C denotes the number of categories for variable two. Note that Dataplot assumes that the categories can be meaningfully ordered (Dataplot assumes a "small" to "large" ordering).

In this case, if variable one denotes "ground truth" and variable two denotes the estimate of ground truth, then we define:

1. A correct value is the case where the estimated category is the same as the ground truth category.

   For this case, we do not distinguish between "true positives" and "true negatives" as we do for the 2x2 case.

2. A false positive is the case where the estimated category is too large.

3. A false negative is the case where the estimated category is too small.

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

None

TRUE POSITIVES	= Compute the proportion of true positives.
TRUE NEGATIVES	= Compute the proportion of true negatives.
FALSE NEGATIVES	= Compute the proportion of false negatives.
POSITIVE PREDICTIVE VALUE	= Compute the positive predictive value.
NEGATIVE PREDICTIVE VALUE	= Compute the negative predictive value.
TEST SENSITIVITY	= Compute the test sensitivity.
TEST SPECIFICITY	= Compute the test specificity.
ODDS RATIO	= Compute the bias corrected log(odds ratio).
ODDS RATIO STANDARD ERROR	= Compute the standard error of the bias corrected log(odds ratio).
RELATIVE RISK	= Compute the relative risk.
STATISTICS PLOT	= Generate a statistic versus subset plot.
BOOTSTRAP PLOT	= Generate a bootstrap plot.
TABULATE	= Perform a tabulation for a specified statistic.

Fleiss, Levin, and Paik (2003), "Statistical Methods for Rates and Proportions," Third Edition, Wiley, chapter 1.

Categorical Data Analysis

2007/04

 
let n = 1
.
let p = 0.2
let y1 = binomial rand numb for i = 1 1 100
let p = 0.1
let y2 = binomial rand numb for i = 1 1 100
.
let p = 0.4
let y1 = binomial rand numb for i = 101 1 200
let p = 0.08
let y2 = binomial rand numb for i = 101 1 200
.
let p = 0.15
let y1 = binomial rand numb for i = 201 1 300
let p = 0.18
let y2 = binomial rand numb for i = 201 1 300
.
let p = 0.6
let y1 = binomial rand numb for i = 301 1 400
let p = 0.45
let y2 = binomial rand numb for i = 301 1 400
.
let p = 0.3
let y1 = binomial rand numb for i = 401 1 500
let p = 0.1
let y2 = binomial rand numb for i = 401 1 500
.
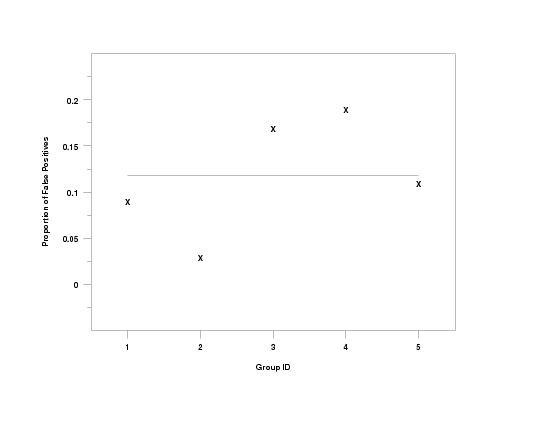
let x = sequence 1 100 1 5
.
let a = false positives y1 y2 subset x = 1
tabulate false positives y1 y2 x
.
label case asis
xlimits 1 5
major xtic mark number 5
minor xtic mark number 0
xtic mark offset 0.5 0.5
ytic mark offset 0.05 0.05
y1label Proportion of False Positives
x1label Group ID
character x blank
line blank solid
.
false positives plot y1 y2 x