DPNTLINE

DPNTLINE (LET)

Library Function

Compute the perpindicular distance between a point and line defined by a point and a slope.

Given a point (X1,Y1) and line defined by (X2,Y2) and the slope s, determine the perpindicular distance between (X1,Y1) and the line.

The formula for this distance is

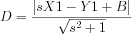
where the line is defined as

Y2 = s*X2 + B
B = Y2 - s*X2

LET <dist> = DPNTLINE(<x1>,<y1>,<x2>,<y2>,<slope>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x1> is a variable or a parameter containing the x coordinates of the first point;
            <y1> is a variable or a parameter containing the y coordinates of the first point;
            <x2> is a variable or a parameter containing the x coordinates of the second point;
            <y2> is a variable or a parameter containing the y coordinates of the second point;
            <slope> is the slope of the line containing (<x2>,<y2>);
            <dist> is a variable or a parameter (depending on what the input arguments are) where the computed perpindicular distances are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DPNTLINE(1,1,0,0,0.5)
LET DIST = DPNTLINE(X1,Y1,X2,Y2,SLOPE)

None

None

Bowyer and Woodwark (1983), "A Programmer's Geometry", Butterworths, pp. 12-13.

ANGRAD	= Return the counter clockwise angle, in radians, of the angle determined by three points.
POINTS IN POLYGON	= Determine whether points are in the interior of a convex polygon.
CONVEX HULL	= Determine the convex hull of a set of points.
TRANSFORM POINTS	= Perform location, scale, and rotation transformation for a set of points.
EXTREME POINTS	= Determine the extreme points of a set of points.
LINE INTERSECTIONS	= Determine the intersection points for a set of lines.
PARALLEL LINE	= Determine the coordinates for a point that defines a parallel line determined by a point and a line defined by two points.
PERPINDICULAR LINE	= Determine the coordinates for a point that defines a perpindicular line determined by a point and a line defined by two points.

Computational Geometry

2012/10

 
skip 25
read convhull.dat x y
.
let y2 x2 = 2d convex hull y x
let xtemp = x2(1)
let ytemp = y2(1)
let y2 = combine y2 ytemp
let x2 = combine x2 xtemp
let x3 = x2
let y3 = y2
let n = size y2
let nm1 = n - 1
retain x2 y2 for i = 1 1 nm1
retain x3 y3 for i = 2 1 n
let slope = slope(x2,y2,x3,y3)
let pdist = dpntline(xtemp,ytemp,x3,y3,slope)
.
set write decimals 4
print "Anchor Point: (^xtemp,^ytemp)"
print " "
print " "
print x3 y3 slope pdist
    

The following output is generated

 
Anchor Point: (0,-2.)
 
 
 
------------------------------------------------------------
             X3             Y3          SLOPE          PDIST
------------------------------------------------------------
         1.0000        -1.7300         0.2700         0.0000
         1.7300        -1.0000         1.0000         0.3650
         2.0000         0.0000         3.7037         0.3674
         1.7300         1.0000        -3.7037         0.6392
         1.0000         1.7300        -1.0000         2.3650
         0.0000         2.0000        -0.2700         3.7282
        -1.0000         1.7300         0.2700         3.7282
        -1.7300         1.0000         1.0000         2.3650
        -2.0000         0.0000         3.7037         0.6392
        -1.7300        -1.0000        -3.7037         0.3674
        -1.0000        -1.7300        -1.0000         0.3650
         0.0000        -2.0000        -0.2700         0.0000