B12PPF

B12PPF (LET)

Library Function

Compute the Burr type 12 percent point function with shape parameters c and k.

The standard Burr type 12 distribution has the following percent point function:

with c and k denoting the shape parameters.

This distribution can be generalized with location and scale parameters in the usual way using the relation

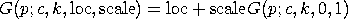
The Burr type 12 distribution is also sometimes referred to as the Singh-Maddala distribution.

LET <y> = B12PPF(<p>,<c>,<k>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable in the interval (0,1);
            <y> is a variable or a parameter (depending on what <p> is) where the computed Burr type 12 ppf value is stored;
            <c> is a positive number, parameter, or variable that specifies the first shape parameter;
            <k> is a positive number, parameter, or variable that specifies the second shape parameter;
            <loc> is a number, parameter, or variable that specifies the location parameter;
            <scale> is a positive number, parameter, or variable that specifies the scale parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <loc> and <scale> are omitted, they default to 0 and 1, respectively.

LET A = B12PPF(0.95,0.2,1.7)
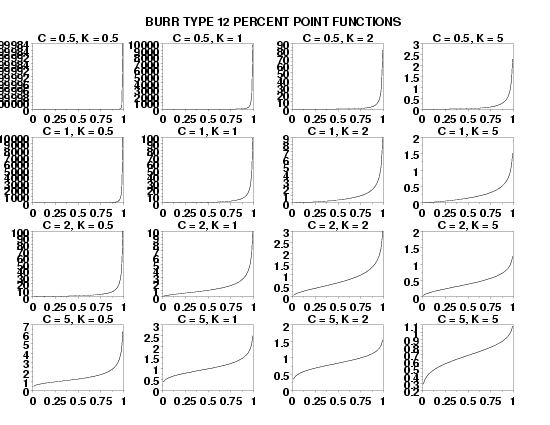
LET Y = B12PPF(X,0.5,2.2,0,5)
PLOT B12PPF(P,2.3,1.4) FOR P = 0.01 0.01 0.99

None

BURR TYPE XII is a synonym for BURR TYPE 12.

B12CDF	= Compute the Burr type 12 cumulative distribution function.
B12PDF	= Compute the Burr type 12 probability density function.
BU2PDF	= Compute the Burr type 2 probability density function.
BU3PDF	= Compute the Burr type 3 probability density function.
BU4PDF	= Compute the Burr type 4 probability density function.
BU5PDF	= Compute the Burr type 5 probability density function.
BU6PDF	= Compute the Burr type 6 probability density function.
BU7PDF	= Compute the Burr type 7 probability density function.
BU8PDF	= Compute the Burr type 8 probability density function.
BU9PDF	= Compute the Burr type 9 probability density function.
B10PDF	= Compute the Burr type 10 probability density function.
B11PDF	= Compute the Burr type 11 probability density function.
RAYPDF	= Compute the Rayleigh probability density function.
WEIPDF	= Compute the Weibull probability density function.
EWEPDF	= Compute the exponentiated Weibull probability density function.

Burr (1942), "Cumulative Frequency Functions", Annals of Mathematical Statistics, 13, pp. 215-232.

Johnson, Kotz, and Balakrishnan (1994), "Contiunuous Univariate Distributions--Volume 1", Second Edition, Wiley, pp. 53-54.

Devroye (1986), "Non-Uniform Random Variate Generation", Springer-Verlang, pp. 476-477.

Distributional Modeling

2007/10

 
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 4 4
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 4
.
LET CVAL = DATA 0.5  1  2  5
LET KVAL = DATA 0.5  1  2  5
.
LOOP FOR IROW = 1 1 4
    LOOP FOR ICOL = 1 1 4
        LET C = CVAL(IROW)
        LET K = KVAL(ICOL)
        TITLE C = ^c, K = ^k
        PLOT B12PPF(P,C,K) FOR P = 0.01  0.01  0.99
    END OF LOOP
END OF LOOP
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Burr Type 12 Percent Point Functions