BU2PDF

BU2PDF (LET)

Library Function

Compute the Burr type 2 probability density function with shape parameter r.

The standard Burr type 2 distribution has the following probability density function:

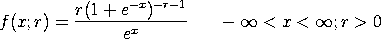
with r denoting the shape parameter.

This distribution can be generalized with location and scale parameters in the usual way using the relation

LET <y> = BU2PDF(<x>,<r>,<loc>,<scale>)
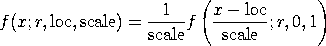
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Burr type 2 pdf value is stored;
            <r> is a positive number, parameter, or variable that specifies the shape parameter;
            <loc> is a number, parameter, or variable that specifies the location parameter;
            <scale> is a positive number, parameter, or variable that specifies the scale parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <loc> and <scale> are omitted, they default to 0 and 1, respectively.

LET A = BU2PDF(0.3,0.2)
LET Y = BU2PDF(X,0.5,0,5)
PLOT BU2PDF(X,2,0,3) FOR X = 0 0.01 5

Burr type 2 random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET R = <value>
LET Y = BURR TYPE 2 RANDOM NUMBERS FOR I = 1 1 N
BURR TYPE 2 PROBABILITY PLOT Y
BURR TYPE 2 PROBABILITY PLOT Y2 X2
BURR TYPE 2 PROBABILITY PLOT Y3 XLOW XHIGH
BURR TYPE 2 KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
BURR TYPE 2 CHI-SQUARE GOODNESS OF FIT Y2 X2
BURR TYPE 2 CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH


The following commands can be used to estimate the r shape parameter for the Burr type 2 distribution:

LET R1 = <value>
LET R2 = <value>
BURR TYPE 2 PPCC PLOT Y
BURR TYPE 2 PPCC PLOT Y2 X2
BURR TYPE 2 PPCC PLOT Y3 XLOW XHIGH
BURR TYPE 2 KS PLOT Y
BURR TYPE 2 KS PLOT Y2 X2
BURR TYPE 2 KS PLOT Y3 XLOW XHIGH


The default values for R1 and R2 are 0.5 and 10.

The probability plot can then be used to estimate the location and scale (location = PPA0, scale = PPA1).

The BOOTSTRAP DISTRIBUTION command can be used to find uncertainty intervals for the parameter estimates based on the ppcc plot and ks plot.

None

BURR TYPE II is a synonym for BURR TYPE 2.

BU2CDF	= Compute the Burr type 2 cumulative distribution function.
BU2PPF	= Compute the Burr type 2 percent point function.
BU3PDF	= Compute the Burr type 3 probability density function.
BU4PDF	= Compute the Burr type 4 probability density function.
BU5PDF	= Compute the Burr type 5 probability density function.
BU5PDF	= Compute the Burr type 6 probability density function.
BU7PDF	= Compute the Burr type 7 probability density function.
BU8PDF	= Compute the Burr type 8 probability density function.
BU9PDF	= Compute the Burr type 9 probability density function.
B10PDF	= Compute the Burr type 10 probability density function.
B11PDF	= Compute the Burr type 11 probability density function.
B12PDF	= Compute the Burr type 12 probability density function.
RAYPDF	= Compute the Rayleigh probability density function.
WEIPDF	= Compute the Weibull probability density function.
EWEPDF	= Compute the exponentiated Weibull probability density function.

Burr (1942), "Cumulative Frequency Functions", Annals of Mathematical Statistics, 13, pp. 215-232.

Johnson, Kotz, and Balakrishnan (1994), "Contiunuous Univariate Distributions--Volume 1", Second Edition, Wiley, pp. 53-54.

Devroye (1986), "Non-Uniform Random Variate Generation", Springer-Verlang, pp. 476-477.

Distributional Modeling

2007/10

 
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
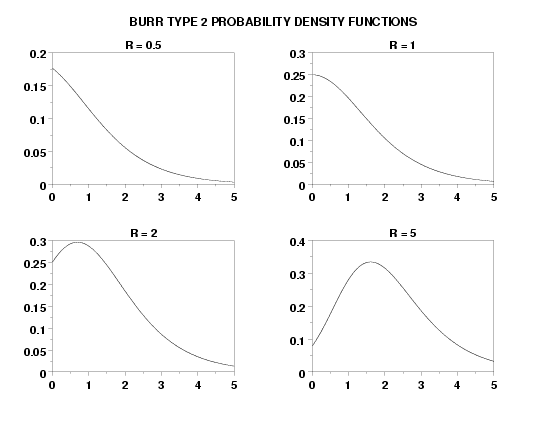
LET R  = 0.5
TITLE R = ^r
PLOT BU2PDF(X,R) FOR X = 0.01  0.01  5
.
LET R  = 1
TITLE R = ^r
PLOT BU2PDF(X,R) FOR X = 0.01  0.01  5
.
LET R  = 2
TITLE R = ^r
PLOT BU2PDF(X,R) FOR X = 0.01  0.01  5
.
LET R  = 5
TITLE R = ^r
PLOT BU2PDF(X,R) FOR X = 0.01  0.01  5
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Burr Type 2 Probability Density Functions
    

 
let r = 2.1
let rsav = r
.
let y = burr type 2 random numbers for i = 1 1 200
let y = 10*y
let amax = maximum y
.
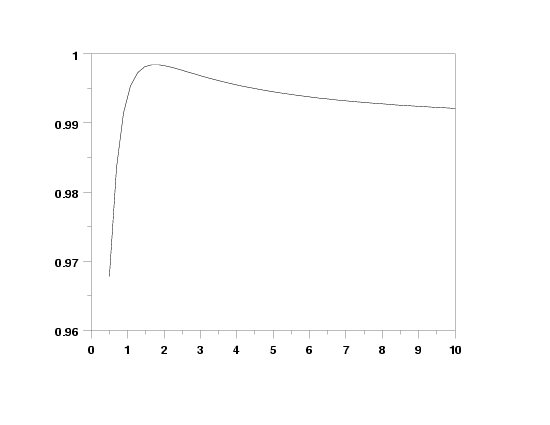
burr type 2 ppcc plot y
let rtemp = shape - 2
let r1 = max(rtemp,0.05)
let r2 = shape + 2
y1label Correlation Coefficient
x1label R
burr type 2 ppcc plot y
let r = shape
justification center
move 50 6
text Rhat = ^r (R = ^rsav)
move 50 2
text Maximum PPCC = ^maxppcc
.
char x
line bl
burr type 2 prob plot y1
move 50 6
text Location = ^ppa0, Scale = ^ppa1
char bl
line so
.
relative hist y
limits freeze
pre-erase off
plot b10pdf(x,r,ppa0,ppa1) for x = 0.01 .01 amax
limits 
pre-erase on
.
let ksloc = ppa0
let ksscale = ppa1
burr type 2 kolmogorov smirnov goodness of fit y
    









                   KOLMOGOROV-SMIRNOV GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            BURR TYPE 2
    NUMBER OF OBSERVATIONS              =      200
  
 TEST:
 KOLMOGOROV-SMIRNOV TEST STATISTIC      =   0.3776631E-01
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       0.086*              ACCEPT H0
                      0.085**
             5%       0.096*              ACCEPT H0
                      0.095**
             1%       0.115*              ACCEPT H0
                      0.114**
  
     *  - STANDARD LARGE SAMPLE APPROXIMATION  ( C/SQRT(N) )
    ** - MORE ACCURATE LARGE SAMPLE APPROXIMATION  ( C/SQRT(N + SQRT(N/10)) )