Next Page Previous Page Home Tools & Aids Search Handbook
5. Process Improvement
5.6. Case Studies
5.6.3. Catapult Case Study

5.6.3.2.

Main Effects
Plot the Data: Dex Scatter Plot The first step in the analysis is to plot the data using the dex scatter plot.

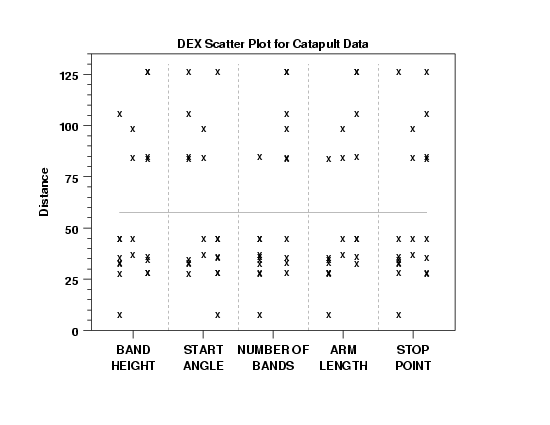
dex scatter plot shows several noteworthy features

Conclusions We can make the following conclusions from the dex scatter plot.
  1. Wide Spread: The most noteworthy aspect of the DEX scatter plot is the wide range of the response. The distance ranges nearly 10 feet: from near-0 to beyond 125 inches. Clearly, therefore, with such a range we have an interesting system. Either we have a system in which the factors and their settings have no effect but is extremely noisy (unlikely), or we have a system in which the factors and settings have a deterministic effect which simply needs to be uncovered (more likely).

  2. Bimodality: Also noteworthy is the bifurcation of the data into 2 regions: below 50 inches and above 80 inches, with a large 30+ inch gap in the middle. Such bimodality is often caused by the presence of discrete (non-continuous) factors in the experiment, which would point an initial finger at factor 1 (band height) and factor 3 (number of bands) as the possible culprits. In any event, the bimodality is glaring and so a side-goal of the analysis is to uncover the reason for its existence.

  3. Settings for Y = 60: The gap from roughly 50 to 80 is of particular concern because one of the stated engineering goals is to determine settings for the 5 factors that would yield a response of 60 inches, and there is no setting in any of the 20 runs that yielded a response anywhere close to Y = 60. The implication is, therefore, that the best setting must come from a derived model and hence additional "pressure" is being put on the model that it have good interpolatory/extrapolatory properties.

  4. Weak Main Factors: Note from the scatter plot that none of the 5 factors is (for one setting) consistently below and then (for the other setting) consistently above the gap. This implies that there is no dominant factor and hence the resulting model will be more complicated and less parsimonious (that is will need many terms).
Plot the Data: Box Plots An alternative is to generate a box plot, which reduces all of the eight data points at a given factor and setting into (in the simplest case) five summary statistics: the minimum, the 25% point, the 50% point (the median), the 75% point, and the maximum. Because of such simplicity, the box plot sometimes manifests the differences in response locations (that is, the factor effects) more clearly that the DEX scatter plot.

the box plot indicates a variance stabilizing transformation may be necessary

Conclusions We can make the following conclusions from the box plot.
  1. Low Settings: Note how certain settings tend to yield low responses. In particular, smaller distances (<= 50 inches) tend to come from

      (X1,X2,X3,X4,X5) = (-,+,-,-,-).

    Further, these settings yield responses which also have low variability. One can conclude, therefore, the the best setting to yield Y = 30 (one of the experiment objectives) will probably be in the vicinity of (-,+,-,-,-).

    2. High Settings: Note that the opposite settings:

      (X1,X2,X3,X4,X5) = (+,-,+,+,+)

    yield responses which are high location and high variability (that is, the distances are much longer, but the responses are also much noisier). This implies that the Y = 90 settings we develop will be much noisier (and hence of much poorer quality) that the Y = 30 settings.

    3. Variance-Stabilizing Transformations: Furthermore, this combination of low location and low variability with high location and high variability is characteristic of a system which violates the constant variability assumption implicit in subsequent least-squares model fitting, and hence provides the first suggestion that a variance-stabilizing transformation (e.g., logarithmic) should be applied to the data prior to further analysis. This transformation issue will be be revisited later.

Check for Main Effects: Dex Mean Plot One of the experimental goals is to identify the most important factors. Specifically we would like to produce a ranked list of such factors, ranked from the most important to the least important. Such "factors" can include main effects, but can in more generality include interactions. The dex mean plot (also known as the main effects plot) is an effective tool for producing such a ranked list for main effects only (no interactions).

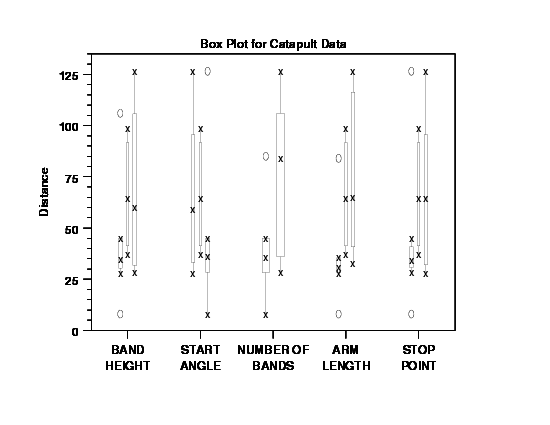
Note that the dex scatter plot and the box plots used all the data including center points. For the dex mean plot, we produce two plots--one with the center points and one without. As is common in the analysis of 2-level designs, we choose for subsequent analyses to omit the center points and to use just the vertices of the 2**(5-1). We hold the center points aside for analysis and for modeling and we will use them at a later time for model validation and confirmation.

In a dex mean plot, the vertical axis is the mean response at a setting (typically this will be the mean of 8 values). One virtue of orthogonal designs (such as the 2**(5-1) utilized here) is that the least squares estimates of the factor effects is identically the difference of the means for each setting. Hence, large differences (steep slopes) that manifest themselves in a dex mean plot implies large estimated factor effects. The dex mean plot provides an easy "eyeball" method for arriving at an initial ranked list of main factors.

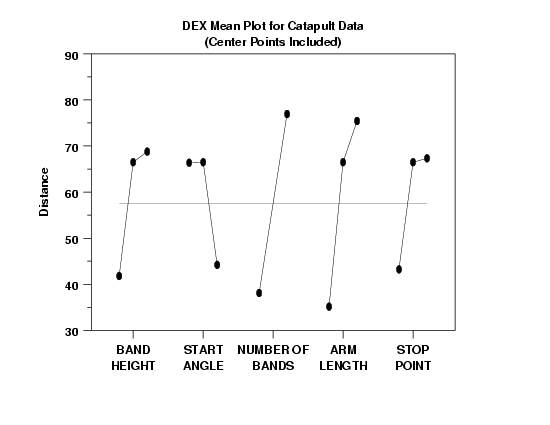
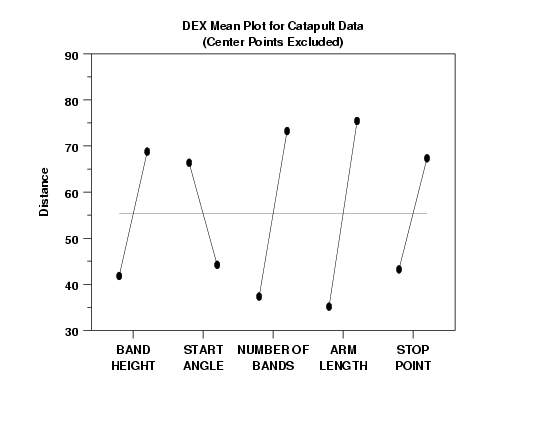
DEX Mean Plot: Center Points Included dex mean plot shows several noteworthy features
DEX Mean Plot: Center Points Excluded dex mean plot shows several noteworthy features
Conclusions We can make the following conclusions from the dex mean plots.
  1. Ranked List of Factors: From the dex mean plot with no center points, we may deduce the ranked list of important factors as

    1. X4 (arm length) (effect = about 40 inches)
    2. X3 (number of bands) (effect = about 35 inches)
    3. X1 (band height) (effect = about 30 inches)
    4. X5 (start point) (effect = about 25 inches)
    5. X2 (stop angle) (effect = about 20 inches)

  2. Lack of Dominant Factors: From the dex mean plot, we note that the factor effects drop off in a slow, near-uniform fashion. This is not typical. It is much more common in engineering experiments to have 1 or 2 factors dominate and the remaining factor effects being 2 to 10 times smaller. That was not the case here. There are 5 possible reasons for this non-dominance:

    1. Engineering reality
    2. Interactions & Confounding
    3. Other Factors
    4. Noisiness (high variance)
    5. Non-constant variance

    These 5 possibilities are now discussed point-by-point.

    1. Engineering Reality: The estimated effects may in fact be accurate, and this may be a factual reflection of the engineering cause-and-effect. Again, this is not usually seen in engineering experiments, but is a possibility.

    2. Interactions and Confounding: Interactions may be important and hence (in fractional factorial designs) may contaminate main effects. However, for the 2**(5-1) fractional factorial design that we have run, main effects are not confounded with any 2-term or 3-term interactions (only 4-term interactions and higher). For many physical systems, the assumption that 4-term interactions and higher are nil (and may be discarded) is invariably safe, and hence for this experiment, contamination via confounding is adjudged not to be the cause.

    3. Other factors: Other factors (besides the 5 we have controlled) may in fact be driving the system. Unfortunately, these other factors may be known or unknown, recorded or not recorded. If there are other factors driving the system, then this is a near-fatal experimental deficiency, and their effect will be smeared over (that is, will bias) the main effects in an unpredictable way. For this experiment, this possibility must still be entertained. In the larger issue, this is detected by the replicated (pseudo-) center points during the experiment, and the post-experiment confirmation runs (replicated) at the best settings (to yield Y = 30, 60, and 90). For the replicated pseudo-center points, the spread is reasonably close (see below) and so there appears no drifiting caused by other factors. Hence for this data, "other factors" is probably not the cause.

    4. Noisy Experiment: Some experiments are intrinsically noisy (for example, fracture and reliability data). If the replication standard deviation (the intrinsic variability the data have under fixed conditions) is high, then that may translate into large and non-discriminating effect estimates. Fortunately, in our experiment design, we designed in some replication (the 2 pseudo-center points (each) at X3 = -1 and X3 = +1) so as to estimate how much intrinsic replication error the catapult experiment has. For the 2 pseudo-center points at (0,0,-1,0,0), the data is Y = 37.5 and 45, and hence the replication standard deviation is 5.303. For the 2 pseudo-center points at (0,0,1,0,0), the data is Y = 84.5 and 99 and so the standard deviation is 9.175. Combining these two estimates, we form a pooled standard deviation of 8.162. Since 8.162 is less than 10% of the total spread of the data (8 to 126.5), a "noisy experiment" is probably not the cause of the large effect estimates.

    5. Non-constant variance: This is the case where the data is partially noisy. That is, it is precise in certain subregions but noisy in other subregions. In particular, for the case where the response variable Y is in a proportionately noisy (low response has low random error but large response has large random error), as opposed to absolutely noisy (all the responses have the same random error), then the settings of each factor which tend to yield large responses (distances) will be noisy, and hence tend to produce longer distances, larger means, and hence larger effect estimates. For this experiment, non-constant variation is plausible and the most likely explanation for the non-discriminating effect estimates. This discussion point will be picked up at a later time.

  3. Settings to Maximize the Response: One of the engineering objectives of this experiment was to find the settings of the 5 factors that would yield Y = 30, 60, and 90. If we temporarily set aside this stated objective, and replace it with the objective: "Find the settings which maximize the response" (which is common in many other engineering experiments), then the dex mean plot assists in answering that question. By noting for each factor as to whether the maximum mean is attained by -1 or +1, we may deduce from the plot that (on the average) the maximal response is attained by

      (X1,X2,X3,X4,X5) = (+1,-1,+1,+1,+1)

    Scanning the raw data table, we note that (+,-,+,+,+) happened by chance to not be one of the design points (since this was a fractional factorial design). However, the design point which yielded the observed maximum response (Y = 126.5) was (+,-,+,+,-). Note that these 2 sets of settings are identical for factors X1 to X4 and differ only in factor X5. Based on the dex mean plot, this suggests that (+,-,+,+,+) may in fact yield a larger response than the observed (+,-,+,+,-). This may be confirmed (or denied) by follow-up confirmation runs at (+,-,+,+,+).

  4. Settings to Yield Y = 30, 60, 90: As for the stated experimental objective of determining best settings to yield Y = 30, 60, and 90, we may deduce that the Y = 90 settings will be in the "vicinity" of the maximum setting: (+,-,+,+,+); the Y = 30 settings will be in the "vicinity" of the converse: (-,+,-,-,-); and the Y = 60 settings are still unknown at this point.
Check for Main Effects: Dex Median Plot The dex median plot is similar to the dex mean plot. Definitionally, each plot point in the dex median plot is the median of all eight points at the given setting (-1 or +1) of the given factor.

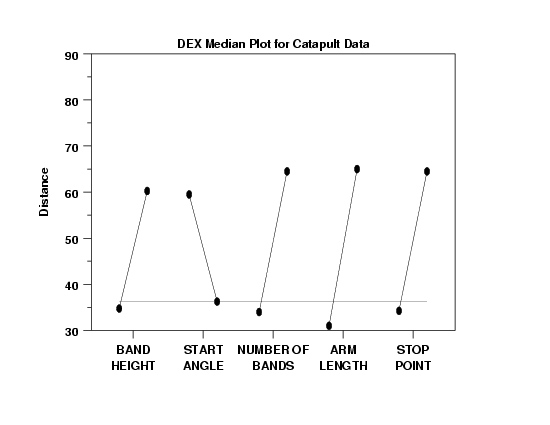
The dex median plot is not usually in the recommended list of analysis techniques for 2-level orthogonal designs. We employ it here because of the aforementioned noting of non-constant variation and how that ties in with skewness. We are specifically generating this plot so as to compare its conclusions with the conclusions of the dex mean plot. However, for formal effect estimation, we still employ the usual least squares estimates which are the difference of the means.

dex median plot shows several noteworthy featurs

Conclusions We can make the following conclusions from the dex median plot.
  1. Skewness and Transformations: The dex median plot indicates that the data is skewed. Note from the dex mean plot that the grand mean of all 16 points is approximately 55, whereas from the dex median plot the grand median is drastically smaller: approximately 36. Further, the location for the higher points has dropped from around 70 (mean) to 60 (median), and the location of the lower points has dropped from around 40 (mean) to around 35 (median). All of these are consistent with skewed data. Skewed data is not fundamentally wrong to analyze. On the other hand, the usual analysis tools and tests are more valid with normal (or at least symmetric) data and so this suggests a transformation to normality (or at least symmetry). Again, a logarithmic transformation is commonly useful to achieve this goal.

  2. Ranked list of factors: Note that the ranked list of factors from the dex mean plot was X4, X3, X1, X5, and X2, whereas the ranked list of factors from the dex median plot is X4, X3, X5, X1, and X2. The consistency and robustness of the X4 and X3 ranking across both plots provides confidence in the importance of these two factors relative to the remaining 3 factors.

  3. Best Settings for Maximum: Although this is not a stated objective of the experiment, note that the settings to yield the maximum on the median is the same (+,-,+,+,+) as the settings to yield the maximum from the dex mean plot.
Check for Main Effect Variability: Dex SD Plot As with the dex median plot, the dex standard deviation plot is not usually generated (or needed). We employ it here to illustrate how it may be usefully interpreted in certain anomalous cases. Each plot point is the simple standard deviation of all eight points at the given setting (-1 or +1) of the given factor.

dex sd plot shows several noteworthy issues

Conclusions We can make the following conclusions from the dex standard deviation plot.
  1. Ranked List of "Noisy" Factors: Factors X3 (number of bands), X4 (arm length), and X1 (band height) all significantly differ in noisiness (by a factor of around 2 in the standard deviation) between the -1 and +1 settings. The +1 settings are about twice as noisy as the -1 setting for all 3 of these factors. Factors X2 (start angle) and X5 (stop angle) have nearly equal variation across their 2 settings.

  2. Non-Constant Variation: It is useful to interpret the dex standard deviation plot in conjunction with the dex mean plot. Note that the settings of the 5 factors which minimize the variability (from the dex standard deviation plot) is (-,+,-,-,-). Note that this is identical to the settings of the 5 factors which minimize the mean (from the dex mean plot). Similarly, large variability is from (+,-,+,+,+) which is identical to large location (+,-,+,+,+). Thus we have a reinforcement of what was seen before, namely that the variation is increasing with the location. This is referred to as non-constant variation and its existence negates the usual coefficient estimation output from future least squares fitting.
Comparison of Plots We have generated five separate plots to assess the main factor effects. We recommend that at a minimum, both the dex scatter plot and dex mean plot be generated for all fractional factorial analyses. The box plot can substitute for the dex scatter plot or be used to complement the dex scatter plot. The box plot becomes easier to interpret than the dex scatter plot as the number of factors, and thus the number of observations, gets larger. In this case, the dex scatter plot and box plot indicated high variabiliity, which was not constant across factors, in the data. For that reason, we complemented the dex mean and scatter plots with a dex median plot and a dex standard deviation plot.

The dex scatter plot (or a box plot) and the dex mean plot are useful first steps in viewing the data from a fractional factorial experiment. The dex mean plot shows the main effects more clearly than the dex scatter plot. However, the dex scatter plot can show more detail, such as the prescence of outliers, that are hidden in the dex mean plot.

Home Tools & Aids Search Handbook Previous Page Next Page