5.6.3.6. Best Settings

5. Process Improvement
5.6. Case Studies
5.6.3. Catapult Case Study

5.6.3.6. Best Settings

One of the experimental objectives was to determine "best" settings for (X1,X2,X3,X4,X5) so as to achieve Y = 30, 60, and 90 inch distances. To solve this problem, we utilize 2 approaches:

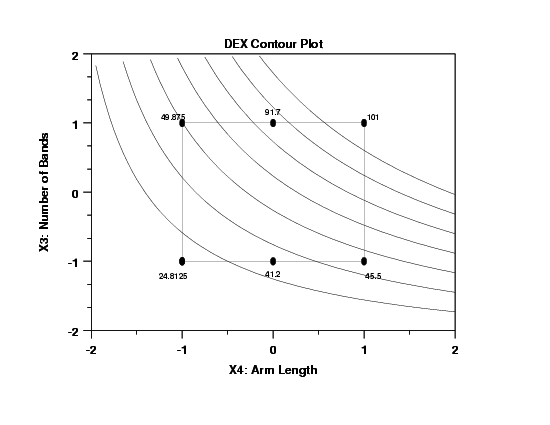
Graphical: DEX Contour Plot
Quantititative: Sorted Data Table

The virtue of these approaches is that they both depend on the data itself, and may be done independently of the previously discussed modeling and any of the deficiencies therein.

Use Two Most Important Factors for the Contour Plot

We first use a dex contour plot to help determine best settings. The only piece of information needed from the prior analysis is the top 2 entrees in the ranked list of factors:

X4 (arm length) (effect = 40.3 inches)
X3 (number of bands) (effect = 35.9 inches)
X1 (band height) (effect = 27.0 inches)
X5 (start point) (effect = 24.0 inches)
X2 (stop angle) (effect = -22.2 inches)
X3*X4 interaction (effect = 15.2 inches)
X1*X4 interaction (effect = 9.4 inches)
X1*X3 interaction (effect = 9.3 inches)

From this table, X4 (arm length) and X3 (number of bands) are the two most important factors. We thus choose to use these two factors as the axes on the contour plot:

X4 (arm length): horizontally
X3 (number of bands): vertically

DEX Contour Plot

The values at the 4 vertices of this data square are obtained by simple averages of the data points. For example, at the vertex (X4 = +1, X3 = -1), the 4 data points from the original data table which have x4 = +1 and X3 = -1 are 33, 85, 45, and 36.5. These 4 values average to 45.5 which becomes the value at that vertex. Similar averages are computed for the other three vertices. For the pseudo-center point at X3 = -1, the data is 45 and 37.5 with the average being 41.25. At the pseudo-center point at X3 = +1, the data is 99 and 84.5 yielding an average of 91.75. The original 20 data points are thus reduced to six mean values. Based on these mean values, the dex contour plot (with contour lines at 30, 40, 50, ..., 90) is as follows:

Conclusions From the DEX Contour Plot

We can make the following conclusions from the dex contour plot.

Curvature and Interactions: The curvature in the contour lines indicates a strong interaction effect between X3 and X4. Referring back to the Yates table ranking, we note that the X3*X4 interaction was in fact the largest of all of the intereactions (with a magnitude of 15.2), and so the above graphical curvilinearity is consistent with prior quantitative results. Note conversely that if the contour curves had been linear, then that would imply a planar model in X3 and X4 with the additional implication that the X3*x4 cross-product effect is near zero.
Cross-Validation: This is the statistical procedure whereby a part (most) of the data is used for estimation and inference, and a second (smaller) part of the data is set aside and is used for validation and the confirmation. Such was used here: contour curves were (by construction) based on the 16 edge data points. The 4 pseudo-center points were not used in the computation of the contour curves. It is known (small residual standard deviation) that the contour curves predict well on the edges. Can we confidently use the model for prediction everywhere else? Anywhere else? In particular, does it predict well interior to the cube? To answer this, let us compare the contour curves to the known data averages at the two pseudo-center points (at X3 = -1 (41.25) and at X3 = +1 (91.75)). If there is a good match, then that gives us confidence in using the edge-based model for interpolation; if not, then the use of the edge-based model is severely restricted. In this case, we note (eyeball) that at the X3 = -1 pseudo-center point, the average is 41.25 and the contour-lined based prediction is about 37 and so the error is approximately 4 inches. For the X3 = +1 pseudo-center point, the average is 91.75 but the contour-lined based prediction is about 75 and so the error in prediction is an overly-large 16 inches. Hence in this case, the contour lines predict well in the vicinity of the X3 = -1 pseudo-center point, but poorly at the X3 = +1 pseudo-center point. This cross-validation is discuraging and hence implies that the model may not be used freely for interpolation, and hence interpolatory best settings based on the model are not to be trusted.
Discrete Factor: Note that the factor X3 (number of bands) is intrinsically discrete (the number of bands is either 1 or 2 and one could not have, e.g., 1.7 bands). Given this, then one may have argue that the contour plots are meaningless. In a very real sense that is correct; on the other hand, the above two conclusions are both correct and the contour plots, discreteness notwithstanding, helped arrive at these two conclusions. In preparation for the upcoming question as to what are the best settings for (X1,X2,X3,X4,X5) for Y = 30, 60, and 90, we make use of the discreteness and relatively high importance of X3 (the second most important factor) to split the data (based on X3= -1 and X3 = +1) and generate the following two contour plots of X1 (the third most important factor) versus X4 (the most important factor)

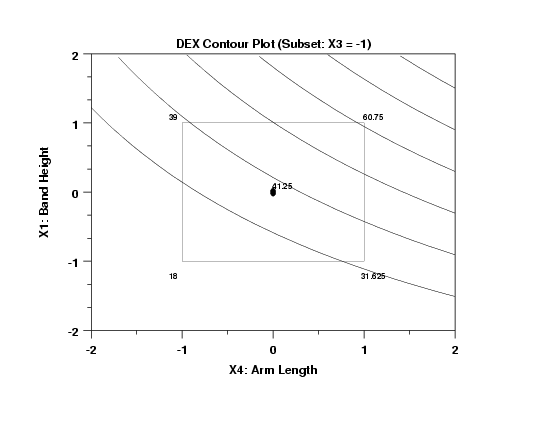
DEX Contour Plot of X4 and X1 with X3 = -1

Conclusions From the X3 = -1 DEX Contour Plot

We can make the following conclusions from the X3 = -1 (that is, the number of bands = 1) dex contour plot.

The curves are relatively linear (implying a relatively small X1*X4 interaction).
The response curves are relatively small (from 30 to 60).
The curves fit the center point relatively well (actual = 41.25; predicted = 37).

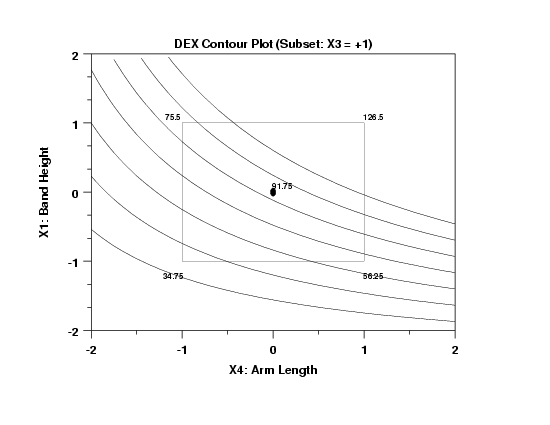
DEX Contour Plot of X4 and X1 with X3 = -1

Conclusions From the X3 = 1 DEX Contour Plot

We can make the following conclusions from the X3 = 1 (that is, the number of bands = 2) dex contour plot.

The curves are curvilinear which implies a large X1*X4 interaction.
The response curves are relatively large (from 40 to 90).
The curves fit the center point poorly (actual = 91.75; predicted = 73).

Additional Conclusions

We can draw the following additional conclusions based on the original dex contour plot and the two additional dex contour plots based on subsets of X3.

Best Settings for Y = 30: Choose the level of the splitting factor first; in this case, since X3 = -1 is more centered on lower values of Y than X3 = +1, and since X3 = -1 has better interpolatory properties than X3 = +1, then choose X3 = -1. Given that, any point along the Y = 30 curve will work. We choose the intersection point of the Y = 30 curve and the bottom of the box (X1 = -1). This yields X4 = +.8 and X1 = -1. This is also near a vertex point with average 31.625. We have 3 out of the 5 settings:
The remaining two settings (for X2 and X5) will be derived later.
Best Settings for Y = 60: Since X3 = -1 has better interpolatory properties than X3 = +1, then choose X3 = -1. As before, any point along' the Y = 60 curve will work. Note that Y = 60 comes very close to the (X4 = +1, X1 = +1) vertex which has an (average) value of 60.75--very close to 60. Unfortunately, the two raw data values going into the 60.75 are quite disparate: 36.5 (from ++-+-) and 85.0 (from +--++). We thus see that the settings for X2 and X5 make a huge difference in the response: (X2 = +1, X5 = -1) yields 36.5 while (X2 = -1, X5 = +1) yields 85.0. We will decide on these two value later, but for now, as before, we have
Best Settings for Y = 90: Since the X3 = -1 contour plot has no values in the vicinity of Y = 90 except for distant extrapolation, we resort to the X3 = +1 plot. On this plot, we could make use of the Y = 90 curve, but since the X3 = +1 case has such poor interpolatory properties, it makes better sense to set aside the biased curves and rely more heavily on the observed data. Note, for example, that the center point for the X3 = +1 contour plot has an average value of 91.75--very close to 90. Note that the data which led to this center point average of 91.75 is from (00100) replicates: 99.0 and 84.5. These 2 data points, even while being collected under identical conditions, still differed by almost 15 inches (with a standard deviation of 10.25 inches). This is large, but it is as good as the data can do. That is, we have two values under replicate conditions symmetrically spanning the desired Y = 90. In conclusion, we choose our best settings for Y = 90 to be
This is primarily a data-based estimate for the best settings, but given that the model performs poorly and yields biased estimates for this X3 = +1 case, such a data-based estimate is the preferred choice.

Sorted Data

Up to this point, there has been a significant effort in obtaining best settings based on graphical tools in conjuntion with best-fit modeling. The last step is a quantitative one and involves a simple ordering of the data (smallest to largest). In the absence of any other techniques, such an ordering is quite useful in terms of determining best settings, especially if the observed data happens to fall in the vicinity of the desired target response values, namely, Y = 30, 60, and 90.

The sorted data (carrying along the settings of X1 to X5 is as follows:


                             RUN  CENT
   Y      X1  X2  X3  X4  X5 SEQ POINT
---------------------------------------
  8.00    -1   1  -1  -1  -1  10     0
 28.00    -1  -1  -1  -1   1   1     0
 28.25     1   1  -1  -1   1   8     0
 28.50     1   1   1  -1  -1  14     0

 33.00    -1  -1  -1   1  -1  12     0
 33.50    -1  -1   1  -1  -1  15     0
 35.00     1  -1  -1  -1  -1   6     0
 36.00    -1   1   1  -1   1  16     0
 36.50     1   1  -1   1  -1  11     0
 37.50     0   0  -1   0   0  19     2
 45.00    -1   1  -1   1   1  18     0
 45.00     0   0  -1   0   0   7     2
 45.00    -1   1   1   1  -1   5     0

 84.00     1  -1   1  -1   1  17     0
 84.50     0   0   1   0   0  13     1
 85.00     1  -1  -1   1   1   9     0

 99.00     0   0   1   0   0   2     1
106.00    -1  -1   1   1   1  20     0
126.50     1  -1   1   1  -1   4     0
126.50     1   1   1   1   1   3     0

Conclusions From the Sorted Data

We can make the following conclusions based on the sorted data.

Bimodlality of the Data: Note that the data naturally splits itself into two regions: 45 and below (13 values), and 84 and above (7 values).
Important Factors:
- X3: Of the 13 low values, 9 have X3 = -1. Of the 7 highest values, 6 have X3 = +1 This kind of strong reversal implies X3 is the most important of the factors.
- X4: Of the 13 lowest values, 7 have X4 = -1. Of the 7 highest values, only 1 has X4 = +1. The 4 lowest values have X4 = -1. The 3 highest values have X4 = +1. X4 is also important (but next so).
- X1: Of the 13 lowest values, 7 have X1 = -1. Of the 7 highest values, only 1 has X1 = +1. The 2 lowest values have X1 = -1. The 2 highest values have X1 = +1. X1 is next in importance.
- X5: Of the 13 lowest values, 7 have X5 = -1. Of the 7 highest values, only 1 has X5 = +1. X5 is next in importance.
- X2: The distribution of -1's and +1's is fairly even. X2 is the least important of the 5 factors.
Best Settings for Y = 30: Based only on the above sorted data, and considering the large replication standard deviation of the data, a good choice for Y = 30 would be the closest data point, namely, 28.5 which comes via
Although this point has the smallest error (28.5 - 30 = -1.5 inches), any of the close points may also be used:
Best Settings for Y = 60: Based only on the above ordered data, no setting yields a response anywhere in the vicinity of Y = 60 and so no data-based best setting is possible. In fact, there is no empirical proof that ANY (possible) settings of the catapult system will yield Y = 60. We generate Y = 60 predicted values based on the fact that we are assuming the model to be of correct form and to be valid over the entire region. The first assumption is questionable and the second is false due to poor interpolatory prediction (especially for X3 = +1).
Best Settings for Y = 90: Based only on the above sorted data, and considering the large replication standard deviation of the data, a good choice for Y = 90 would be the closest data point, namely, 85 which comes via
Although this point has the smallest error: 85 - 90 = -5 any of the close points may also be used:

Recommendations

In summary, we make the following recommentdations.

Best Settings for Y = 30: If simplicity is preferred, use the "Sorted Data" solution (+ + + - -) which yielded a close to 30 data value (28.5). This solution has the advantage that it is model-free.
A better solution (but it involves collecting more data) is to use the "DEX Contour Plot" solution of (- ? - + ?). The values of X2 and X5 are unknown. There are 4 cases for X2 and X5:
Make 2 additional runs to collect data at -+-+- and ---++ and then draw the X5 versus X2 DEX contour plot and use any value of X2 and X5 along the Y = 30 contour curve.
Best Settings for Y = 60: Since there is no data anywhere close to Y = 60, there is no "Sorted Data" recommendation.
The recommended solution involves collecting more data. data) is to use the "DEX Contour Plot" solution of (+ ? - + ?). The values of X2 and X5 are unknown. There are 4 cases for X2 and X5:
Make 2 additional runs to collect data at +--+- and ++-++ and then draw the X5 versus X2 DEX contour plot and use any value of X2 and X5 along the Y = 60 contour curve. Further, for this noisy region it would be preferable to collect a center point at +0-+0, and even better still to replicate that center point to determine a local estimate of noise.
Best Settings for Y = 90: If simplicity is preferred, use the "Sorted Data" solution (0 0 + 0 0) which yielded an average close to the desired 90 value (91.5). This solution has the advantage that it is model-free.
Since the 2 data values (84.5 and 99) that went into that replicate average are quite disparate, then sampling anywhere else in the vicinity will probably be for naught. Hence in this case, the simplest solution (at the replicated center point for X3 = +1) is also the recommended best solution.