5. Process Improvement
5.5. Advanced topics
5.5.5. How do you optimize a process?
5.5.5.2. Multiple response case

5.5.5.2.1.

Multiple response: Path of steepest ascent

A weighted priority strategy is described using the path of steepest ascent for each response
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

An example using the weighted priority method
 
 

 

When the responses exhibit adequate linear fit (i.e., the response models are all linear) the question is to find a direction or path that simultaneously considers the individual paths of maximum improvement and balances them in some way. This case is addressed next. 

When there is a mix of linear and higher order responses, or when all empirical response models are of higher order, see sections 5.5.5.2.2 and 5.5.5.2.3. The desirability method (section 5.5.5.2.2 ) can also be used when all response models are linear.

Procedure: Path of Steepest Ascent, Multiple Responses.

1. Compute the gradients 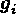 of all responses as explained in section 5.5.5.1.1. If one of the responses is clearly of primary interest compared to all the others, use only the gradient of this response and follow the procedure of section 5.5.5.1.1. Otherwise, continue with step 2.
2. Determine relative priorities 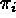 for each of the k responses. Then, the weighted gradient for the search direction is given by

 

 
 
 



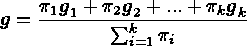
 and the weighted direction is

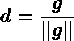
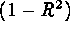The confidence cone for the direction of maximum improvement explained in section 5.6.1.1 can be used to weight down "poor'' response models that provide very wide cones and unreliable directions. Since the width of the cone is proportional to , we can use

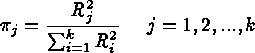
Given a weighted direction of maximum improvement we can follow the single response steepest ascent procedure as in section 5.5.5.1.1. by selecting points with coordinates 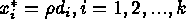 . These and related issues are explained more fully in Del Castillo (1996).

Example: Path of Steepest Ascent, Multiple Response Case

Suppose the response model:

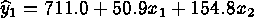
with 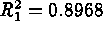, represents the average yield of a production process obtained from a replicated factorial experiment in the two controllable factors (in coded units). From the same experiment, a second response model for the process standard deviation of the yield is obtained and given by

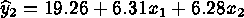
with 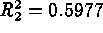. We wish to maximize the mean yield while minimizing the standard deviation of the yield.

Step 1: compute the gradients:

 
 

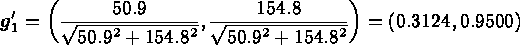
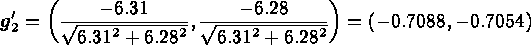
(recall we wish to minimize ).

Step 2: find relative priorities.

Since there are no clear priorities, we use the quality of fit as priority:

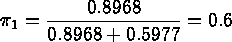
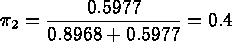
Then, the weighted gradient is

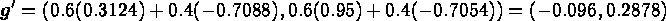
which, after normalizing it (by dividing each coordinate by 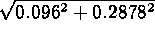) gives the weighted direction

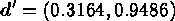
Thus, if we want to move 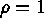 coded units along the path of maximum improvement, we will set

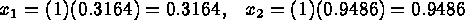
in the next run or experiment.