ZETPPF

ZETPPF (LET)

Library Function

Compute the Zeta percent point function.

The zeta distribution has the following probability mass function:

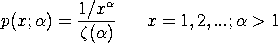
with denoting the shape parameter and denoting the Riemann zeta function

Some sources parameterize this distribution with s = - 1 (so that the distribution is defined for s > 0).

The cumulative distribution is computed by summing the probability mass function. The percent point function is the inversre of the cumulative distribution function and is obtained by computing the cumulative distribution function until the desired probability is reached. The zeta distribution can have very long tails as the value of alpha gets close to 1. Dataplot will return an error message if the percent point value exceeds the maximum machine integer value.

LET <y> = ZETPPF(<p>,<alpha>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a variable, number, or parameter in the interval (0,1);
            <alpha> is a number or parameter greater than 1 that specifies the shape parameter;
            <y> is a variable or a parameter where the computed zeta ppf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = ZETPPF(0.95,1.5)
LET Y = ZETPPF(P1,2.3)
PLOT ZETPPF(P,2.3) FOR X = 0 0.01 0.95

None

None

ZETCDF	= Compute the Zeta cumulative distribution function.
ZETPDF	= Compute the Zeta probability mass function.
ZIPPDF	= Compute the Zipf cumulative distribution function.
YULPDF	= Compute the Yule probability mass function.
BGEPDF	= Compute the beta-geometric (Waring) probability mass function.
BTAPDF	= Compute the Borel-Tanner probability mass function.
DLGPDF	= Compute the logarithmic series probability mass function.
INTEGER FREQUENCY TABLE	= Generate a frequency table at
COMBINE FREQUENCY TABLE	= Combine low frequency classes in a frequency table.
KS PLOT	= Generate a minimum chi-square plot.
MAXIMUM LIKELIHOOD	= Perform maximum likelihood estimation for a distribution.

Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 465-471.

Devroye (1986), "Non-Uniform Random Variate Generation", Springer-Verlang, New York.

Distributional Modeling

2006/5

multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
case asis
label case asis
title case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label displacement 17
x1label displacement 12
.
x1label Probability
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
y1label X
line blank
spike on
.
multiplot 2 2
.
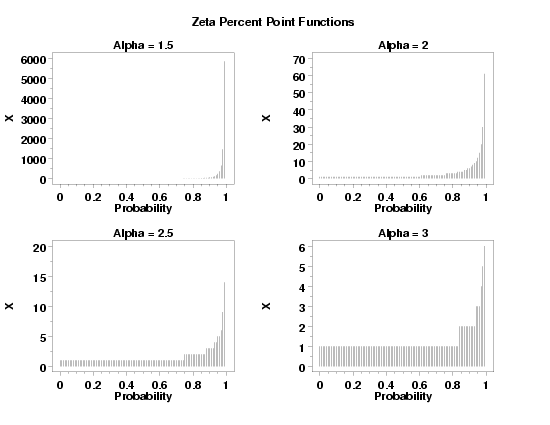
let alpha = 1.5
title Alpha = ^alpha
plot zetppf(p,alpha) for p = 0  0.01  0.99
.
let alpha = 2.0
title Alpha = ^alpha
plot zetppf(p,alpha) for p = 0  0.01  0.99
.
let alpha = 2.5
title Alpha = ^alpha
plot zetppf(p,alpha) for p = 0  0.01  0.99
.
let alpha = 3.0
title Alpha = ^alpha
plot zetppf(p,alpha) for p = 0  0.01  0.99
.
end of multiplot
.
justification center
move 50 97
text Zeta Percent Point Functions