MIECDF

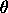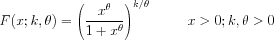
The Mielke's beta-kappa distribution can be generalized with location and scale parameters (u and , respectively) using the formula

LET <y> = MIECDF(<x>,<k>,<theta>,<u>,<beta>)
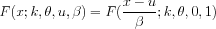
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable;
            <k> is a number, parameter, or variable that specifies the first shape parameter;
            <theta> is a number, parameter, or variable that specifies the second shape parameter;
            <u> is a number, parameter, or variable that specifies the location parameter;
            <beta> is a number, parameter, or variable that specifies the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Mielke's beta-kappa cdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The <u> and <beta> parameters are optional.

LET A = MIECDF(3,0.5,2,0,1.5)
LET X2 = MIECDF(X1,K,THETA)

None

None

MIEPDF	= Compute Miekle's beta-kappa probability density function.
MIEPPF	= Compute Miekle's beta-kappa percent point function.
KAPPDF	= Compute the Kappa probability density function.
BETPDF	= Compute the beta probability density function.
FPDF	= Compute the F probability density function.
GAMPDF	= Compute the gamma probability density function.
NCBPDF	= Compute the non-central beta probability density function.
NORPDF	= Compute the normal probability density function.

Hosking and Wallis (1997), "Regional Frequency Analysis", Cambridge University Press, Appendix A10.

Johnson, Kotz, and Balakrishnan (1994), "Continuous Univariate Distributions: Volume 2", 2nd. Ed., John Wiley and Sons, p. 351.

Distributional Modeling

1996/1: Original implementation as KAPCDF
2008/5: Renamed as MIECDF (KAPPDF now refers to regular Kappa distribution)
2008/5: Beta parameter now properly treated as a scale parameter (was previously treated as a shape parameter)

 
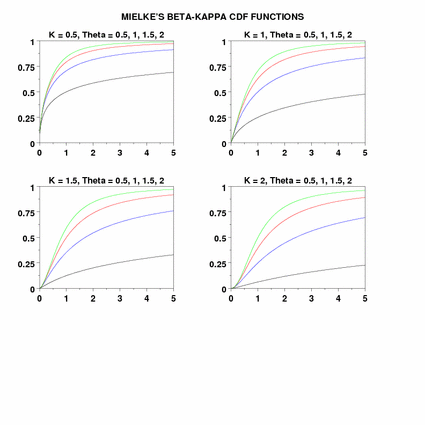
LET KP = DATA 0.5  1  1.5  2.0
LET T1 = 0.5
LET T2 = 1
LET T3 = 1.5
LET T4 = 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 95 95
MULTIPLOT SCALE FACTOR 2
TITLE CASE ASIS
TITLE OFFSET 2
X3LABEL
LINE COLOR BLACK BLUE RED GREEN
.
LOOP FOR LL = 1 1 4
   LET K = KP(LL)
   TITLE K = ^K, Theta = 0.5, 1, 1.5, 2
   PLOT MIECDF(X,K,T1) FOR X = 0.01  0.01  5  AND
   PLOT MIECDF(X,K,T2) FOR X = 0.01  0.01  5  AND
   PLOT MIECDF(X,K,T3) FOR X = 0.01  0.01  5  AND
   PLOT MIECDF(X,K,T4) FOR X = 0.01  0.01  5
END OF LOOP
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Mielke's Beta-Kappa CDF Functions