MATCDF
Name:
Type:
Purpose:
Compute the classical matching cumulative distribution
function.
Description:
The classical matching distribution has the following
probability mass function:
with k a non-negative integer denoting the number of
items parameter.
The cumulative distribution function is computed by
summing the probability density function.
Syntax:
LET <y> = MATCDF(<x>,<k>)
<SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter containing
values between 0 and <k>;
<k> is a number or parameter that defines the upper
limit of the matching distribution;
<y> is a variable or a parameter (depending on what
<x> is) where the computed cdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
LET A = MATCDF(3,20)
LET Y = MATCDF(X,100)
Note:
For sufficiently large values of k, the classical
matching distribution can be accurately approximated with a
Poisson distribution with
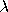 = 1.
Dataplot computes MATCDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATCDF using the Poisson cdf with = 1.
Dataplot computes MATCDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATCDF using the Poisson cdf with
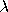 = 1. = 1.
Default:
Synonyms:
Related Commands:
|
MATPDF
|
= Compute the matching probability mass function.
|
|
MATPPF
|
= Compute the matching percent point function.
|
|
POIPDF
|
= Compute the Poisson probability mass function.
|
|
LCTPDF
|
= Compute the leads in coin tossing probability mass
function.
|
|
DISPDF
|
= Compute the discrete uniform probability mass function.
|
|
LOSPDF
|
= Compute the lost games probability mass function.
|
|
ARSPDF
|
= Compute the arcsine probability density function.
|
|
BETPDF
|
= Compute the beta probability density function.
|
|
UNIPDF
|
= Compute the uniform probability mass function.
|
Reference:
Johnson, Kotz, and Kemp (1992), "Univariate Discrete
Distributions", Second Edition, Wiley, pp. 409-410.
Feller (1957), "Introduction to Probability Theory",
Third Edition, John Wiley and Sons, pp. 107-109.
Applications:
Implementation Date:
Program:
TITLE CASE ASIS
TITLE Matching Cumulative Distribution Function CR() ...
(N = 50)
LABEL CASE ASIS
Y1LABEL Probability
X1LABEL X
LINE BLANK
SPIKE ON
TIC OFFSET UNITS SCREEN
TIC OFFSET 3 3
PLOT MATCDF(X,50) FOR X = 0 1 50
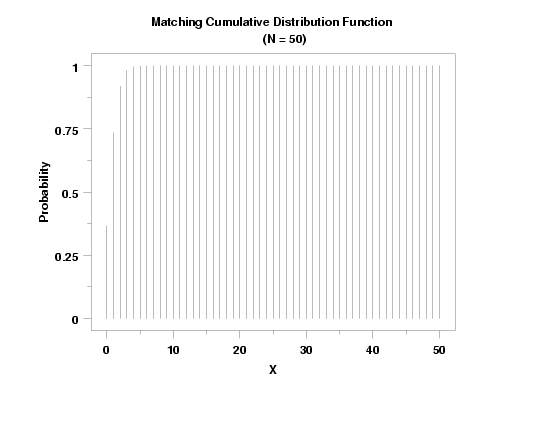
Date created: 6/20/2006
Last updated: 6/20/2006
Please email comments on this WWW page to
[email protected].
|


![p(x;k) = (1/x!)*SUM[i=1 to k-x][(-1)^i/i!] x = 0, 1, 2, ..., k](eqns/matpdf.gif)
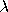 = 1.
Dataplot computes MATCDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATCDF using the Poisson cdf with
= 1.
Dataplot computes MATCDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATCDF using the Poisson cdf with
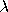 = 1.
= 1.
