LCTPDF

LCTPDF (LET)

Library Function

Compute the leads in coin tossing probability mass function.

The formula for the leads in coin tossing probability mass function is

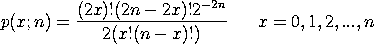
with n a non-negative integer denoting the shape parameter.

Given 2n coin tosses, let 2k denote the last coin toss for which the cumulative number of heads and tails were equal (0 ≤ k ≤ n). The leads in coin tossing distribution is the distribution of k. We use 2n and 2k since a tie can only occur on an even number toss.

Feller (see Further Information below) points out that the common belief that in a long coin-tossing game that each player will be on the winning side approximately half the time with frequent lead changes is in fact erroneous. Frequent lead changes implies that k should be close to n. However, for this distribution the probability that x = k is equal to the probability that x = n - k. The implication of this is that with probability 1/2 no equalization will occur in the second half of the game regardless of the length of the game.

The mean and variance of the leads in coin tossing distribution are:

mean =

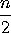
variance =

The leads in coin tossing distribution is also known as the discrete arcsine distribution.

LET <y> = LCTPDF(<x>,<n>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter containing values between 0 and <n>;
            <n> is a number or parameter that defines the upper limit of the leads in coin tossing distribution;
            <y> is a variable or a parameter (depending on what <x> is) where the computed pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = LCTPDF(3,20)
LET Y = LCTPDF(X,100)

For a number of commands utilizing the leads in coin tossing distribution, it is convenient to bin the data. There are two basic ways of binning the data.
1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:
   LET AMIN = MINIMUM Y
   LET AMAX = MAXIMUM Y
   LET AMIN2 = AMIN - 0.5
   LET AMAX2 = AMAX + 0.5
   CLASS MINIMUM AMIN2
   CLASS MAXIMUM AMAX2
   CLASS WIDTH 1
   LET Y2 X2 = BINNED
   

2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands
   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
   

   If you already have equal width bins data, you can use the commands

   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
   

   The MINSIZE parameter defines the minimum class frequency. The default value is 5.

You can generate leads in coin tossing random numbers, probability plots, and chi-square goodness of fit tests with the following commands:
LET NSIZE = VALUE
LET N = <value>
LET Y = LEADS IN COIN TOSSING RANDOM NUMBERS ...
            FOR I = 1 1 N


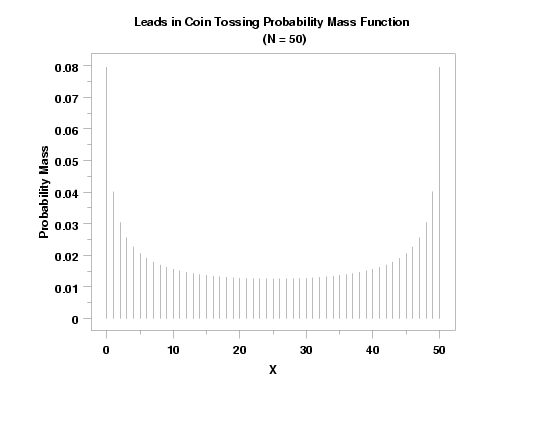
LEADS IN COIN TOSSING PROBABILITY PLOT Y
LEADS IN COIN TOSSING PROBABILITY PLOT Y2 X2
LEADS IN COIN TOSSING PROBABILITY PLOT Y3 XLOW XHIGH


LEADS IN COIN TOSSING CHI-SQUARE GOODNESS OF FIT Y
LEADS IN COIN TOSSING CHI-SQUARE GOODNESS OF FIT Y2 X2
LEADS IN COIN TOSSING CHI-SQUARE GOODNESS OF FIT ...
            Y3 XLOW XHIGH


Dataplot does not provide any explicit parameter estimation methods. For this distribution, we simply subtract the minimum value (so the data starts at zero) and then use the maximum value as the estimate of N. We can then apply goodness of fit tests (i.e., the probability plot or the chi-square goodness of fit) to see if the leads in coin tossing is an appropriate distribution.

None

None

LCTCDF	= Compute the leads in coin tossing cumulative distribution function.
LCTPPF	= Compute the leads in coin tossing percent point function.
DISPDF	= Compute the discrete uniform probability mass function.
MATPDF	= Compute the matching probability mass function.
LOSPDF	= Compute the lost games probability mass function.
ARSPDF	= Compute the arcsine probability density function.
BETPDF	= Compute the beta probability density function.
UNIPDF	= Compute the uniform probability mass function.

Feller (1957), "Introduction to Probability Theory", Third Edition, John Wiley and Sons, pp. 78-84.

Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 274-275.

Distributional Modeling

2006/6

 
TITLE CASE ASIS
TITLE Leads in Coin Tossing Probability Mass Function CR() ...
      (N = 50)
LABEL CASE ASIS
Y1LABEL Probability Mass
X1LABEL X
LINE BLANK
SPIKE ON
TIC OFFSET UNITS SCREEN
TIC OFFSET 3 3
PLOT LCTPDF(X,50) FOR X = 0 1 50