SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

GLSPPF

Name:
    GLSPPF (LET)
Type:
    Library Function
Purpose:
    Compute the generalized logarithmic series percent point function.
Description:
    The generalized logarithmic series distribution has the following probability mass function:

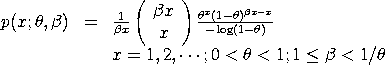
      p(x;theta,beta) = (1/(beta*x))*(beta*x x)theta**x*(1-theta)**(beta*x-x)/ (-LOG(1-theta)) x = 1, 2, ...; 0 < theta < 1; 1 <= beta < -1/theta

    with theta and beta denoting the shape parameters.

    The cumulative distribution function is computed using the following recurrence relation given on pages 228-229 of Consul and Famoye:

      p(x+1;theta,beta) = (beta - x/(x+1))*theta*(1-theta)^(beta-1)* PROD[j=1 to x-1][(1+beta/(beta*x - j))*p(x;theta,beta)

    with

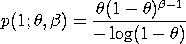
      p(1;theta,beta) = theta*(1-theta)**(beta-1)/(-LOG(1-theta))

      p(2;theta,beta) = (beta-(1/2))*theta*(1-theta)^(beta-1)*p(1;theta,beta)

    The percent point function is computed by summing the above recurence relation until the the specified probability is obtained.

Syntax:
    LET <y> = GLSPDF(<p>,<theta>,<beta>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <p> is a positive integer variable, number, or parameter in the range (0,1);
                <theta> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
                <beta> is a number, parameter, or variable that specifies the second shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed generalized logarithmic series ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = GLSPPF(0.95,0.5,1.4)
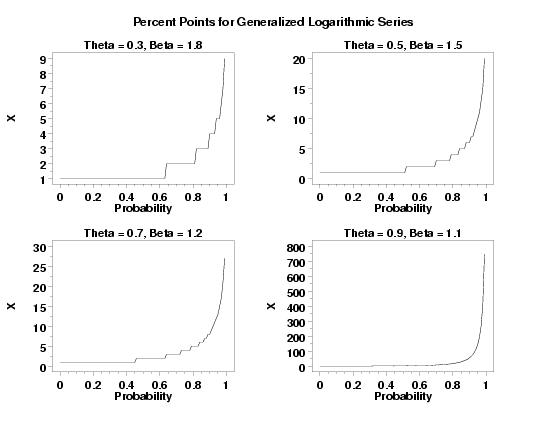
    LET Y = GLSPPF(P,0.3,1.6)
    PLOT GLSPPF(P,0.3,1.6) FOR P = 0 0.01 0.99
Default:
    None
Synonyms:
    None
Related Commands:
    GLSCDF = Compute the generalized logarithmic series cumulative distribution function.
    GLSPDF = Compute the generalized logarithmic series probability mass function.
    DLGPDF = Compute the logarithmic series probability mass function.
    YULPDF = Compute the Yule probability mass function.
    ZETPDF = Compute the Zeta probability mass function.
    BGEPDF = Compute the beta geometric probability mass function.
    POIPDF = Compute the Poisson probability mass function.
    BINPDF = Compute the binomial probability mass function.
Reference:
    Consul and Famoye (2006), "Lagrangian Probability Distribution", Birkhauser, chapter 11.
Applications:
    Distributional Modeling
Implementation Date:
    2006/8
Program: 
     
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
x1label Probability
y1label X
.
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
.
multiplot 2 2
.
title Theta = 0.3, Beta = 1.8
plot glsppf(p,0.3,1.8) for p = 0  0.01  0.99
.
title Theta = 0.5, Beta = 1.5
plot glsppf(p,0.5,1.5) for p = 0  0.01  0.99
.
title Theta = 0.7, Beta = 1.2
plot glsppf(p,0.7,1.2) for p = 0  0.01  0.99
.
title Theta = 0.9, Beta = 1.1
plot glsppf(p,0.9,1.1) for p = 0  0.01  0.99
.
end of multiplot
.
justification center
move 50 97
text Percent Points for Generalized Logarithmic Series
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].