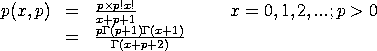YULPDF

YULPDF (LET)

Library Function

Compute the Yule probability mass function.

The Yule distribution has the following probability mass function:

with p denoting the shape parameter and 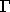denoting the gamma function (HELP GAMMA for details).

Dataplot computes the Yule probability density function using the log gamma function. The Yule distribution has increasingly long tails as p goes to zero. Currently, Dataplot limits the Yule pdf function to the case where p >= 0.1.

LET <y> = YULPDF(<x>,<p>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative integer number, parameter, or variable;
            <p> is a positive number, parameter, or variable that specifies the shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Yule pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = YULPDF(3,1.5)
LET A = YULPDF(X,P)
PLOT YULPDF(X,2) FOR X = 0 1 50

The Yule is a special case of the Waring distribution. Specifically,
YULPDF(X,P) = WARPDF(X,P-1,1)

The following commands for generating random numbers, probability plots, and goodness of fit statistics for the Yule distribution are available:
LET P = <value>
LET Y = YULE RANDOM NUMBERS FOR I = 1 1 N
YULE PROBABILITY PLOT Y
YULE CHI-SQUARE GOODNESS OF FIT Y


The following graphical methods for estimating the shape parameter are available:

YULE PPCC PLOT Y
YULE KS PLOT Y


Our experience indicates that the KS PLOT is more effective than the PPCC PLOT for estimating the shape parameter.

The follwing command

YULE MAXIMUM LIKELIHOOD Y

can be used to generate the following estimates of the shape parameter:

1. The method of moments:
   

   with 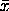denoting the sample mean. Note that this method will never generate an estimate less than 1 (the mean is undefined for p < 1 for the Yule distribution).

2. The method of zero frequency and sample mean:
   

   with N and f1 denoting the sample size and the observed first frequency.

   This method is only useful for values of the shape parameter > 1.

3. The method of maximum likelihood:

   The maximum likelihood estimate is the solution of the following equation:

   

   with N denoting the sample size, V_k the cumulative frequency from k upwards, and 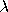the maximum frequency.

   Then the parameter, p, of the Yule distribution is

   p = C - 1.

   These estimation methods are discussed in detail in the Irwin article (see the Reference section belows).

None

None

YULCDF	= Compute the Yule cumulative distribution function.
YULPPF	= Compute the Yule percent point function.
WARPDF	= Compute the Waring probability density function.
BBNPDF	= Compute the beta-binomial probability density function.
GEOPDF	= Compute the geometric probability density function.
NBPDF	= Compute the negative binomial probability density function.
HYPPDF	= Compute the hypergeometric probability density function.

"Discrete Univariate Distributions", Second Edition, Johnson, Kotz, and Kemp, John Wiley & Sons, 1994 (pp. 274-279).

"Mathematcs in Medical and Biological Statistics", J. O. Irwin, Journal of the Royal Statistical Society, A, 1963, pp. 1-44.

Distributional Modeling

2004/4

 
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
TITLE AUTOMATIC
X1LABEL X
Y1LABEL PROBABILITY
TITLE SIZE 3
PLOT YULPDF(X,0.5) FOR X = 0 1 50
PLOT YULPDF(X,1) FOR X = 0 1 50
PLOT YULPDF(X,1.5) FOR X = 0 1 50
PLOT YULPDF(X,2) FOR X = 0 1 50
END OF MULTIPLOT