SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

BTAPPF

Name:
    BTAPPF (LET)
Type:
    Library Function
Purpose:
    Compute the Borel-Tanner percent point function.
Description:
    Given a single queue with random arrival times of customers at constant rate l, constant service time beta, and k initial customers, the Borel-Tanner distribution is the distribution of the total number of customers served before the queue vanishes.

    The probability mass function of the Borel-Tanner distribution is

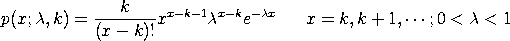
      p(x;lambda,k) = k*EXP(-lambda*x)*(lambda*x)**(x-k)/(x*(x-k)!), x >= k, 0 < lambda < 1

    with lambda and k denoting the shape parameters. The k shape parameter is a positive integer and lambda = lbeta.

    The cumulative distribution function is computed by summing the probability mass function. The percent point function is the inverse of the cumulative distribution function and is obtained by computing the cumulative distribution function until the specified probability is reached.

Syntax:
    LET <y> = BTAPPF(<p>,<lambda>,<k>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <p> is a variable, number, or parameter in the range (0,1);
                <lambda> is a number or parameter in the range (0,1) that specifies the first shape parameter;
                <k> is a number or parameter denoting a positive integer that specifies the first shape parameter;
                <y> is a variable or a parameter where the computed Borel-Tanner ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = BTAPPF(0.95,0.5,3)
    LET Y = BTAPPF(P1,0.3,2)
    PLOT BTAPPF(P,0.4,2) FOR P = 0 0.01 0.99
Default:
    None
Synonyms:
    None
Related Commands:
    BTACDF = Compute the Borel-Tanner cumulative distribution function.
    BTAPDF = Compute the Borel-Tanner probability mass function.
    POIPDF = Compute the Poisson probability mass function.
    HERPDF = Compute the Hermite probability mass function.
    BINPDF = Compute the binomial probability mass function.
    NBPDF = Compute the negative binomial mass density function.
    GEOPDF = Compute the geometric probability mass function.
Reference:
    Haight and Breuer (1960), "The Borel-Tanner Distribution", Biometrika, 47, pp. 143-150.

    Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 394-396.

Applications:
    Distributional Modeling
Implementation Date:
    2006/5
Program: 
     
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label Probability
x1label X
.
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
line blank
spike on
.
multiplot 2 2
.
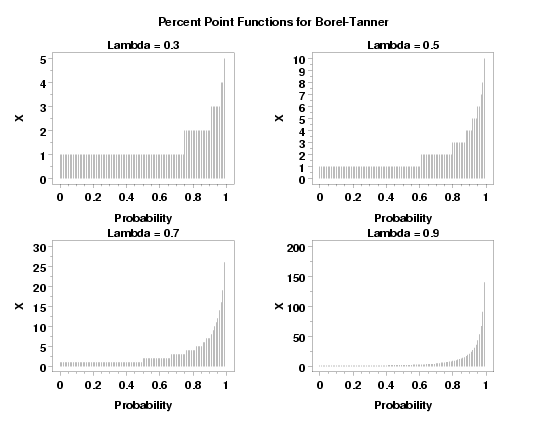
title Lambda = 0.3
plot btappf(p,0.3,1) for p = 0  0.01  0.99
.
title Lambda = 0.5
plot btappf(p,0.5,1) for p = 0  0.01  0.99
.
title Lambda = 0.7
plot btappf(p,0.7,1) for p = 0  0.01  0.99
.
title Lambda = 0.9
plot btappf(p,0.9,1) for p = 0  0.01  0.99
.
end of multiplot
.
justification center
move 50 97
text Percent Point Functions for Borel-Tanner
    plot generated by sample program

Date created: 6/5/2006
Last updated: 6/5/2006
Please email comments on this WWW page to [email protected].