SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

COEFFICIENT OF VARIATION TEST

Name:
    COEFFICIENT OF VARIATION TEST
Type:
    Analysis Command
Purpose:
    Perform either a one sample coefficient of variation test or a two sample coefficient of variation test.
Description:
    The coefficient of variation is defined as the ratio of the standard deviation to the mean

      \( \mbox{cv} = \frac{\sigma} {\mu} \)

    where σ and μ denote the population standard deviation and population mean, respectively. The sample coefficient of variation is defined as

      \( \mbox{cv} = \frac{s} {\bar{x}} \)

    where s and \( \bar{x} \) denote the sample standard deviation and sample mean respectively.

    The coefficient of variation should typically only be used for ratio data. That is, the data should be continuous and have a meaningful zero. Although the coefficient of variation statistic can be computed for data that is not on a ratio scale, the interpretation of the coeffcient of variation may not be meaningful. Currently, this command is only supported for non-negative data. If the response variable contains one or more negative numbers, an error message will be returned.

    The one sample coefficient of variation tests whether the coefficient of variation is equal to a given value. Note that this can be for either a single sample or for the common coefficient for multile groups of data (it is assummed the groups have equal population coefficient of variation values).

      H0: γ = γ0
      Ha: γ ≠ γ0

    The test statistic is

      \( \sum_{i}^{k}{\frac{(n_{i} - 1) u_{i}} {\theta_{0}}} \)

    where

      k = the number of groups
      \( u_{i} \) = \( \frac{c_{i}^{2}} {1 + c_{i}^{2} (n_{i} - 1)} \)
      ci = coefficient of variation for the i-th group
      ni = sample size for the i-th group
      θ0 = \( \frac{ \gamma_{0}^{2}} {1 + \gamma_{0}^{2}} \)

    where γ is the common coefficient of variation and γ0 is the hypothesized value.

    This statistic is compared to a chi-square with \( \sum_{i}^{k}{n_{i} - 1} \) degrees of freedom. The most common usage is the case for a single group (i.e., k = 1).

    The two sample coefficient of variation tests whether two distinct samples have equal, but unspecified, coefficients of variations. As with the single sample case, each of the two samples can consist of either a single group or multiple groups of data.

      H0: γ1 = γ2
      Ha: γ1 ≠ γ2

    The test statistic is

      \( F = \frac {\mbox{NUM}} {\mbox{DENOM}} \)

    where

      \( \mbox{NUM} = \frac {\sum_{i}^{k}{(n_{1i} - 1) u_{1i}}} {\sum_{i}^{k}{n_{1i} - 1}} \)

      \( \mbox{DENOM} = \frac {\sum_{i}^{k}{(n_{2i} - 1) u_{2i}}} {\sum_{i}^{k}{n_{2i} - 1}} \)

    where

      k1 = the number of groups for sample one
      k2 = the number of groups for sample two
      \( u_{ri}\) = \( \frac{c_{ri}^{2}} {1 + c_{ri}^{2}*(n_{ri} - 1)/n_{ri}} \)
      \( c_{ri} \) = coefficient of variation for the i-th group and the r-th sample
      \( n_{ri} \) = the sample size for the i-the group and the r-th sample
      r = 1, 2 (i.e., the two samples)

    when k1 = k2 = 1, the test simplifies to

      \( F = \frac{c_{1}^{2}/(1 + c_{1}^{2}(n_{1} - 1)/n_{1})} {c_{2}^{2}/(1 + c_{2}^{2}(n_{2} - 1)/n_{2})} \)

    This statistic is compared to the F distribution with \( \sum_{i=1}^{k_{1}}{n_{1i} -1} \) and \( \sum_{i=1}^{k_{2}}{n_{2i} -1} \) degrees of freedom.

    The test implemented here was proposed by Forkman (see the References below). There are a number of alternative tests (see the paper by Krishnamooorthy and Lee in the References section). Simulations by Forkman and also by Krishnamoorthy and Lee indicate that the Forkman test has good nominal coverage and reasonable power.

Syntax 1:
    ONE SAMPLE COEFFICIENT OF VARIATION TEST <y> <x> <gamma0>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y> is the response variable;
                <x> is the optional group-id variable;
                <gamma0> is a parameter that specifies the hypothesized value;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax performs a two-tailed test.

    If there are no groups in the data, the group-id variable can be omitted.

    The <gamma0> can either be given on this command or specified before entering this command by entering

      LET GAMMA0 = <value>

    If the <x> variable is given, it should have the same number of rows as the <y> variable.

Syntax 2:
    ONE SAMPLE COEFFICIENT OF VARIATION <LOWER/UPPER> TAILED
                            TEST <y> <x> <gamma0>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y> is the response variable;
                <x> is the optional group-id variable;
                <gamma0> is a parameter that specifies the hypothesized value;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax performs a one-tailed test. If LOWER is entered, then the alternate hypothesis is

      Ha: gamma < gamma0

    If UPPER is entered, then the alternative hypothesis is

      Ha: gamma > gamma0

    If there are no groups in the data, the group-id variable can be omitted.

    The <gamma0> can either be given on this command or specified before entering this command by entering

      LET GAMMA0 = <value>

    If the <x> variable is given, it should have the same number of rows as the <y> variable.

Syntax 3:
    TWO SAMPLE COEFFICIENT OF VARIATION TEST <y1> <x1> <y2> <x2>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y1> is the first response variable;
                <x1> is the optional first group-id variable;
                <y2> is the second response variable;
                <x2> is the optional second group-id variable;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax performs a two-tailed test.

    If there are no groups in the data, the group-id variables can be omitted. However, if a group-id variable is specified for one response variable, it should also be specified for the second response variable. If one of the response variables has groups but the other response variable does not, then a group-id variable can be created that has all values equal to 1.

    The <y1> and <x1> variables should have the same number of rows. Likewise the <y2> and <x2> variables should have the same number of rows. However, <y1> and need not have the same number of rows.

Syntax 4:
    TWO SAMPLE COEFFICIENT OF VARIATION <LOWER/UPPER> TAILED
                            TEST <y1> <x1> <y2> <x2>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y1> is the first response variable;
                <x1> is the optional first group-id variable;
                <y2> is the second response variable;
                <x2> is the optional second group-id variable;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax performs a one-tailed test. If LOWER is entered, then the alternate hypothesis is

      Ha: gamma1 < gamma2

    If UPPER is entered, then the alternative hypothesis is

      Ha: gamma1 > gamma2

    If there are no groups in the data, the group-id variable can be omitted.

    If there are no groups in the data, the group-id variables can be omitted. However, if a group-id variable is specifiend for one response variable, it should also be specified for the second response variable. If one of the response variables has groups but the other response variable does not, then a group-id variable can be created that has all values equal to 1.

    The <y1> and <x1> variables should have the same number of rows. Likewise the <y2> and <x2> variables should have the same number of rows. However, <y1> and <y2> need not have the same number of rows.

Examples:
    LET GAMMA0 = 0.1
    ONE SAMPLE COEFFICIENT OF VARIATION TEST Y GAMMA0
    ONE SAMPLE COEFFICIENT OF VARIATION TEST Y X GAMMA0
    ONE SAMPLE COEFFICIENT OF VARIATION UPPER TAILED TEST ...
                Y X GAMMA0
    ONE SAMPLE COEFFICIENT OF VARIATION TEST Y X GAMMA0 ...
                SUBSET X > 2

    TWO SAMPLE COEFFICIENT OF VARIATION TEST Y1 Y2
    TWO SAMPLE COEFFICIENT OF VARIATION TEST Y1 X1 Y2 X2
    TWO SAMPLE COEFFICIENT OF VARIATION LOWER TAILED TEST Y1 Y2

Note:
    A table of confidence limits is printed for alpha levels of 50.0, 80.0, 90.0, 95.0, 99.0, and 99.9.
Note:
    In addition to the COEFFICIENT OF VARIATION CONFIDENCE LIMIT command, the following commands can also be used:

      LET A = ONE SAMPLE COEFFICIENT OF VARIATION TEST ...
                  Y X
      LET A = ONE SAMPLE COEFFICIENT OF VARIATION TEST ...
                  CDF Y X
      LET A = ONE SAMPLE COEFFICIENT OF VARIATION TEST ...
                  PVALUE Y X
      LET A = ONE SAMPLE COEFFICIENT OF VARIATION LOWER ...
                  PVALUE Y X
      LET A = ONE SAMPLE COEFFICIENT OF VARIATION UPPER ...
                  PVALUE Y X

      LET A = TWO SAMPLE COEFFICIENT OF VARIATION TEST ...
                  Y1 Y2
      LET A = TWO SAMPLE COEFFICIENT OF VARIATION TEST ...
                  CDF Y1 Y2
      LET A = TWO SAMPLE COEFFICIENT OF VARIATION TEST ...
                  PVALUE Y1 Y2
      LET A = TWO SAMPLE COEFFICIENT OF VARIATION LOWER ...
                  PVALUE Y1 Y2
      LET A = TWO SAMPLE COEFFICIENT OF VARIATION UPPER ...
                  PVALUE Y1 Y2

    The LOWER PVALUE and UPPER PVALUE refer to the p-values based on lower tailed and upper tailed tests, respectively.

    For the one sample test, these statistics can be computed from summary data as well

      LET A = SUMMARY ONE SAMPLE COEFFICIENT OF VARIATION ...
                  TEST YMEAN YSD YN
      LET A = SUMMARY ONE SAMPLE COEFFICIENT OF VARIATION ...
                  CDF YMEAN YSD YN
      LET A = SUMMARY ONE SAMPLE COEFFICIENT OF VARIATION ...
                  PVALUE

    where YMEAN, YSD, and YN are arrays that contain the sample means, sample standard deviations, and sample sizes, respectively.

    In addition to the above LET commands, built-in statistics are supported for 20+ different commands (enter HELP STATISTICS for details).

Note:
    As mentioned above, there are a number of tests that have been proposed. For the two sample test with no groups for the samples, Dataplot also supports the Miller test. This test statistic is given by

      \( \frac {c_{1} - c_{2}} {\sqrt{\frac{c^{2}}{2(n_{1} - 1)} + \frac{c^{4}}{n_{1} - 1} + \frac{c^{2}}{2(n_{2} - 1)} + \frac{c^{4}}{n_{2} - 1}}} \)

    where

      n1 = = the sample size for sample one
      c1 = the sample coefficient of variation for sample one
      n2 = = the sample size for sample two
      c2 = the sample coefficient of variation for sample two
      c = \( \frac{(n_{1} - 1)c_{1} + (n_{2} - 1)c_{2}} {n_{1} + n_{2} - 2} \)

    To use the Miller test, enter the command (before the TWO SAMPLE COEFFICENT OF VARIATION TEST command)

      SET TWO SAMPLE COEFFICIENT OF VARIATION TEST MILLER

    To reset the default Forkman test, enter

      SET TWO SAMPLE COEFFICIENT OF VARIATION TEST FORKMAN
Default:
    None
Synonyms:
    None
Related Commands: References:
    Forkman (2009), "Estimator and Tests for Common Coefficients of Variation in Normal Distributions", Communications in Statistics - Theory and Methods, Vol. 38, pp. 233-251.

    Miller (1991), "Asymptotic Test Statistics for Coefficient of Variation", Communications in Statistics - Theory and Methods, Vol. 20, pp. 3351-3363.

    McKay (1932), "Distributions of the Coefficient of Variation and the Extended 't' Distribution", Journal of the Royal Statistical Society, Vol. 95, pp. 695-698.

    Krishnamoorthy and Lee (2014), "Improved Tests for the Equality of Normal Coefficients of Variation", Computational Statistics, Vol. 29, pp. 215-232.

Applications:
    Confirmatory Data Analysis
Implementation Date:
    2017/06
Program 1: 
     
. Step 1:   Read the data
.
skip 25
read gear.dat y x
skip 0
set write decimals 6
.
. Step 2:   Define plot control
.
title case asis
title offset 2
label case asis
.
y1label Coefficient of Variation
x1label Group
title Coefficient of Variation for GEAR.DAT
let ngroup = unique x
xlimits 1 ngroup
major x1tic mark number ngroup
minor x1tic mark number 0
tic mark offset units data
x1tic mark offset 0.5 0.5
y1tic mark label decimals 3
.
character X
line blank
.
.
. Step 3:   Plot the coefficient of variation over the batches
.
set statistic plot reference line average
coefficient of variation plot y x
.
. Step 4:   Demonstrate the LET commands for the test statistics
.           using raw data
.
let gamma0 = 0.005
let statval = one sample coef of variation test         y x
let statcdf = one sample coef of variation test cdf     y x
let pvalue  = one sample coef of variation test pvalue  y x
let pvall   = one sample coef of variation lower pvalue y x
let pvalu   = one sample coef of variation upper pvalue y x
print statval statcdf pvalue pvall pvalu
.
. Step 4:   Demonstrate the LET commands for the test statistics
.           using summary data
.
set let cross tabulate collapse
let ymean = cross tabulate mean y x
let ysd   = cross tabulate sd   y x
let yn    = cross tabulate size   x
.
let statval2 = summary one sample coef of variation test    ymean ysd yn
let statcdf2 = summary one sample coef of variation cdf     ymean ysd yn
let pvalue2  = summary one sample coef of variation pvalue  ymean ysd yn
print statval2 statcdf2 pvalue2
.
. Step 5:   Hypothesis test for common coefficient of variation
.
let gamma0 = 0.005
one sample coefficient of variation test y x
one sample coefficient of variation upper tail test y x
one sample coefficient of variation lower tail test y x
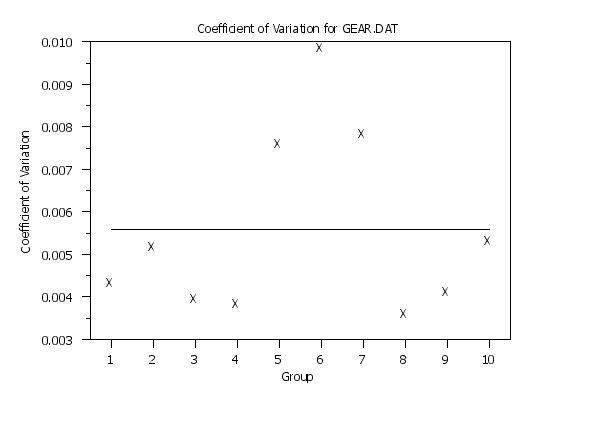
    plot generated by sample program

    The following output is generated. 

     PARAMETERS AND CONSTANTS--

    STATVAL --     127.554980
    STATCDF --       0.994327
    PVALUE  --       0.011346
    PVALL   --       0.994327
    PVALU   --       0.005673
 

 PARAMETERS AND CONSTANTS--

    STATVAL2--     127.554980
    STATCDF2--       0.994327
    PVALUE2 --       0.011346


            Forkman One Sample Coefficient of Variation Test
 
Response Variable: Y
Group-ID Variable: X
 
H0: Coefficient of Variation Equal       0.005000
Ha: Coefficient of Variation Not Equal   0.005000
 
Summary Statistics:
Total Number of Observations:            100
Number of Groups:                        10
Number of Groups Included in Test:       10
Sample Common Coefficient of Variation:  0.005953
 
Test:
Gamma0:                                  0.005000
Test Statistic Value:                    127.554980
Degrees of Freedom:                      90
CDF Value:                               0.994327
P-Value (2-tailed test):                 0.011346
P-Value (lower-tailed test):             0.994327
P-Value (upper-tailed test):             0.005673
 
 
            Two-Tailed Test
 
H0: Gamma = Gamma0; Ha: Gamma <> Gamma0
---------------------------------------------------------------------------
                                        Lower          Upper           Null
   Significance           Test       Critical       Critical     Hypothesis
          Level      Statistic          Value          Value     Conclusion
---------------------------------------------------------------------------
          50.0%     127.554980      80.624665      98.649932         REJECT
          80.0%     127.554980      73.291090     107.565009         REJECT
          90.0%     127.554980      69.126030     113.145270         REJECT
          95.0%     127.554980      65.646618     118.135893         REJECT
          99.0%     127.554980      59.196304     128.298944         ACCEPT
          99.9%     127.554980      52.275778     140.782281         ACCEPT
 
 
            Forkman One Sample Coefficient of Variation Test
 
Response Variable: Y
Group-ID Variable: X
 
H0: Coefficient of Variation Equal       0.005000
Ha: Coefficient of Variation >           0.005000
 
Summary Statistics:
Total Number of Observations:            100
Number of Groups:                        10
Number of Groups Included in Test:       10
Sample Common Coefficient of Variation:  0.005953
 
Test:
Gamma0:                                  0.005000
Test Statistic Value:                    127.554980
Degrees of Freedom:                      90
CDF Value:                               0.994327
P-Value (2-tailed test):                 0.011346
P-Value (lower-tailed test):             0.994327
P-Value (upper-tailed test):             0.005673
 
 
            Upper One-Tailed Test
 
H0: Gamma = Gamma0; Ha: Gamma > Gamma0
------------------------------------------------------------
                                                        Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic      Value (>)     Conclusion
------------------------------------------------------------
          50.0%     127.554980      89.334218         REJECT
          80.0%     127.554980     101.053723         REJECT
          90.0%     127.554980     107.565009         REJECT
          95.0%     127.554980     113.145270         REJECT
          99.0%     127.554980     124.116319         REJECT
          99.9%     127.554980     137.208354         ACCEPT
 
 
            Forkman One Sample Coefficient of Variation Test
 
Response Variable: Y
Group-ID Variable: X
 
H0: Coefficient of Variation Equal       0.005000
Ha: Coefficient of Variation <           0.005000
 
Summary Statistics:
Total Number of Observations:            100
Number of Groups:                        10
Number of Groups Included in Test:       10
Sample Common Coefficient of Variation:  0.005953
 
Test:
Gamma0:                                  0.005000
Test Statistic Value:                    127.554980
Degrees of Freedom:                      90
CDF Value:                               0.994327
P-Value (2-tailed test):                 0.011346
P-Value (lower-tailed test):             0.994327
P-Value (upper-tailed test):             0.005673
 
 
            Lower One-Tailed Test
 
H0: Gamma = Gamma0; Ha: Gamma < Gamma0
------------------------------------------------------------
                                                        Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic      Value (<)     Conclusion
------------------------------------------------------------
          50.0%     127.554980      89.334218         ACCEPT
          80.0%     127.554980      78.558432         ACCEPT
          90.0%     127.554980      73.291090         ACCEPT
          95.0%     127.554980      69.126030         ACCEPT
          99.0%     127.554980      61.754079         ACCEPT
          99.9%     127.554980      54.155244         ACCEPT
Program 2: 
     
. Step 1:   Read the data
.
skip 25
read auto83b.dat y1 y2
skip 0
set write decimals 6
retain y2 subset y2 > 0
.
. Test for equal coefficient of variation
.
let statval = two sample coef of variation test         y1 y2
let statcdf = two sample coef of variation test cdf     y1 y2
let pvalue  = two sample coef of variation test pvalue  y1 y2
let pvall   = two sample coef of variation lower pvalue y1 y2
let pvalu   = two sample coef of variation upper pvalue y1 y2
print statval statcdf pvalue pvall pvalu
.
. Test for equal coefficient of variation
.
two sample coefficient of variation test y1 y2
two sample coefficient of variation lower tail test y1 y2
two sample coefficient of variation upper tail test y1 y2
set two sample coefficient of variation test miller
two sample coefficient of variation test y1 y2
two sample coefficient of variation lower tail test y1 y2
two sample coefficient of variation upper tail test y1 y2
    The following output is generated. 
     PARAMETERS AND CONSTANTS--

    STATVAL --       2.384724
    STATCDF --       0.999992
    PVALUE  --       0.000015
    PVALL   --       0.999992
    PVALU   --       0.000008
 
            Forkman Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 <> gamma2
 
Sample One Summary Statistics:
Total Number of Observations:            249
Number of Groups Included:               1
Sample Mean:                             20.144578
Sample Standard Deviation:               6.414699
Sample Coefficient of Variation:         0.318433
 
Sample Two Summary Statistics:
Total Number of Observations:            79
Number of Included Groups:               1
Sample Mean:                             30.481013
Sample Standard Deviation:               6.107710
Sample Coefficient of Variation:         0.200378
 
Forkman Test Statistic Value:            2.384724
Degrees of Freedom                       248
Degrees of Freedom                       78
CDF Value:                               0.999992
P-Value (2-tailed test):                 0.000015
P-Value (lower-tailed test):             0.999992
P-Value (upper-tailed test):             0.000008
 
 
            Forkman Two Sample Test for Equal Coefficient of Variations
 
H0: gamma1 = gamma2; Ha: gamma1 <> gamma2
---------------------------------------------------------------------------
                                        Lower          Upper           Null
   Significance           Test       Critical       Critical     Hypothesis
          Level      Statistic          Value          Value     Conclusion
---------------------------------------------------------------------------
          50.0%       2.384724       0.889585       1.140474         REJECT
          80.0%       2.384724       0.798111       1.280145         REJECT
          90.0%       2.384724       0.748580       1.373470         REJECT
          95.0%       2.384724       0.708464       1.461059         REJECT
          99.0%       2.384724       0.636939       1.652378         REJECT
          99.9%       2.384724       0.563977       1.913576         REJECT
 
 
            Forkman Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 < gamma2
 
Sample One Summary Statistics:
Total Number of Observations:            249
Number of Groups Included:               1
Sample Mean:                             20.144578
Sample Standard Deviation:               6.414699
Sample Coefficient of Variation:         0.318433
 
Sample Two Summary Statistics:
Total Number of Observations:            79
Number of Included Groups:               1
Sample Mean:                             30.481013
Sample Standard Deviation:               6.107710
Sample Coefficient of Variation:         0.200378
 
Forkman Test Statistic Value:            2.384724
Degrees of Freedom                       248
Degrees of Freedom                       78
CDF Value:                               0.999992
P-Value (2-tailed test):                 0.000015
P-Value (lower-tailed test):             0.999992
P-Value (upper-tailed test):             0.000008
 
 
            Lower One-Tailed Test
 
H0: gamma1 = gamma2; Ha: gamma1 < gamma2
------------------------------------------------------------
                                                        Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic      Value (<)     Conclusion
------------------------------------------------------------
          50.0%       2.384724       1.005895         REJECT
          80.0%       2.384724       0.863240         REJECT
          90.0%       2.384724       0.798111         REJECT
          95.0%       2.384724       0.748580         REJECT
          99.0%       2.384724       0.664874         REJECT
          99.9%       2.384724       0.583430         REJECT
 
 
            Forkman Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 > gamma2
 
Sample One Summary Statistics:
Total Number of Observations:            249
Number of Groups Included:               1
Sample Mean:                             20.144578
Sample Standard Deviation:               6.414699
Sample Coefficient of Variation:         0.318433
 
Sample Two Summary Statistics:
Total Number of Observations:            79
Number of Included Groups:               1
Sample Mean:                             30.481013
Sample Standard Deviation:               6.107710
Sample Coefficient of Variation:         0.200378
 
Forkman Test Statistic Value:            2.384724
Degrees of Freedom                       248
Degrees of Freedom                       78
CDF Value:                               0.999992
P-Value (2-tailed test):                 0.000015
P-Value (lower-tailed test):             0.999992
P-Value (upper-tailed test):             0.000008
 
 
            Forkman Two Sample Test for Equal Coefficient of Variations
 
H0: gamma1 = gamma2; Ha: gamma1 <> gamma2
------------------------------------------------------------
                                        Lower           Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic          Value     Conclusion
------------------------------------------------------------
          50.0%       2.384724       1.005895         ACCEPT
          80.0%       2.384724       1.177041         ACCEPT
          90.0%       2.384724       1.280145         ACCEPT
          95.0%       2.384724       1.373470         ACCEPT
          99.0%       2.384724       1.571455         ACCEPT
          99.9%       2.384724       1.835646         ACCEPT
 
 
THE FORTRAN COMMON CHARACTER VARIABLE TWO SAMP HAS JUST BEEN SET TO MILL
 
            Miller Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 <> gamma2
 
Sample One Summary Statistics:
Number of Observations:                    249
Sample Mean:                               20.144578
Sample Standard Deviation:                 6.414699
Sample Coefficient of Variation:           0.318433
 
Sample Two Summary Statistics:
Number of Observations:                    79
Sample Mean:                               30.481013
Sample Standard Deviation:                 6.107710
Sample Coefficient of Variation:           0.200378
 
Miller Test Statistic Value:               4.100052
CDF Value:                                 0.999979
P-Value (2-tailed test):                   0.000041
P-Value (lower-tailed test):               0.999979
P-Value (upper-tailed test):               0.000021
 
 
            Miller Two Sample Test for Equal Coefficient of Variations
 
H0: gamma1 = gamma2; Ha: gamma1 <> gamma2
---------------------------------------------------------------------------
                                        Lower          Upper           Null
   Significance           Test       Critical       Critical     Hypothesis
          Level      Statistic          Value          Value     Conclusion
---------------------------------------------------------------------------
          50.0%       4.100052      -0.674490       0.674490         REJECT
          80.0%       4.100052      -1.281552       1.281552         REJECT
          90.0%       4.100052      -1.644854       1.644854         REJECT
          95.0%       4.100052      -1.959964       1.959964         REJECT
          99.0%       4.100052      -2.575829       2.575829         REJECT
          99.9%       4.100052      -3.290527       3.290527         REJECT
 
 
            Miller Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 < gamma2
 
Sample One Summary Statistics:
Number of Observations:                    249
Sample Mean:                               20.144578
Sample Standard Deviation:                 6.414699
Sample Coefficient of Variation:           0.318433
 
Sample Two Summary Statistics:
Number of Observations:                    79
Sample Mean:                               30.481013
Sample Standard Deviation:                 6.107710
Sample Coefficient of Variation:           0.200378
 
Miller Test Statistic Value:               4.100052
CDF Value:                                 0.999979
P-Value (2-tailed test):                   0.000041
P-Value (lower-tailed test):               0.999979
P-Value (upper-tailed test):               0.000021
 
 
            Lower One-Tailed Test
 
H0: gamma1 = gamma2; Ha: gamma1 < gamma2
------------------------------------------------------------
                                                        Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic      Value (<)     Conclusion
------------------------------------------------------------
          50.0%       4.100052       0.000000         REJECT
          80.0%       4.100052      -0.841621         REJECT
          90.0%       4.100052      -1.281552         REJECT
          95.0%       4.100052      -1.644854         REJECT
          99.0%       4.100052      -2.326348         REJECT
          99.9%       4.100052      -3.090232         REJECT
 
 
            Miller Two Sample Test for Equal Coefficient of Variations
 
First Response Variable:  Y1
Second Response Variable: Y2
 
H0: Population Coefficients of Variation
    Are Equal (gamma1 = gamma2)
Ha: gamma1 > gamma2
 
Sample One Summary Statistics:
Number of Observations:                    249
Sample Mean:                               20.144578
Sample Standard Deviation:                 6.414699
Sample Coefficient of Variation:           0.318433
 
Sample Two Summary Statistics:
Number of Observations:                    79
Sample Mean:                               30.481013
Sample Standard Deviation:                 6.107710
Sample Coefficient of Variation:           0.200378
 
Miller Test Statistic Value:               4.100052
CDF Value:                                 0.999979
P-Value (2-tailed test):                   0.000041
P-Value (lower-tailed test):               0.999979
P-Value (upper-tailed test):               0.000021
 
 
            Miller Two Sample Test for Equal Coefficient of Variations
 
H0: gamma1 = gamma2; Ha: gamma1 <> gamma2
------------------------------------------------------------
                                        Lower           Null
   Significance           Test       Critical     Hypothesis
          Level      Statistic          Value     Conclusion
------------------------------------------------------------
          50.0%       4.100052       0.000000         ACCEPT
          80.0%       4.100052       0.841621         ACCEPT
          90.0%       4.100052       1.281552         ACCEPT
          95.0%       4.100052       1.644854         ACCEPT
          99.0%       4.100052       2.326348         ACCEPT
          99.9%       4.100052       3.090232         ACCEPT
Date created: 06/27/2017
Last updated: 12/11/2023
Please email comments on this WWW page to alan.heckert@nist.gov.