1.4. EDA Case Studies
1.4.2. Case Studies
1.4.2.8. Heat Flow Meter 1
1.4.2.8.2. |
Graphical Output and Interpretation |
- Determine if the univariate model:
-
\( Y_{i} = C + E_{i} \)
is appropriate and valid.
- Determine if the typical underlying assumptions for an
"in control" measurement process are valid. These assumptions
are:
- random drawings;
- from a fixed distribution;
- with the distribution having a fixed location; and
- the distribution having a fixed scale.
- Determine if the confidence interval
-
\( \bar{Y} \pm 2s/\sqrt{N} \)
is appropriate and valid where s is the standard deviation of the original data.
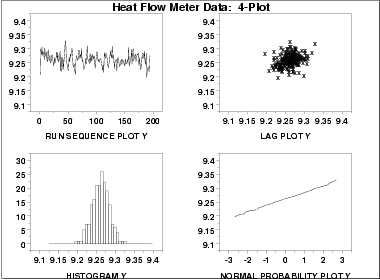
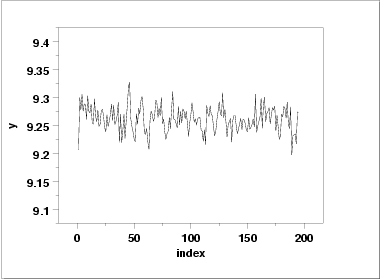
- The run sequence plot
(upper left) indicates that the data do not
have any significant shifts in location or scale over time.
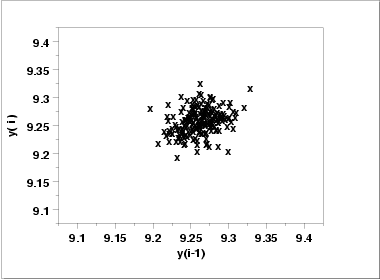
- The lag plot (upper right)
does not indicate any non-random pattern in the data.
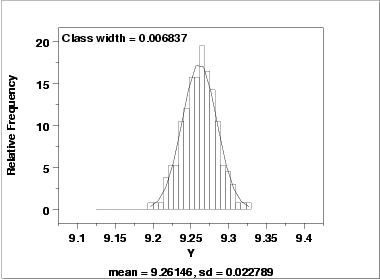
- The histogram (lower
left) shows that the data are reasonably symmetric, there does
not appear to be significant outliers in the tails, and it
seems reasonable to assume that the data are from approximately
a normal distribution.
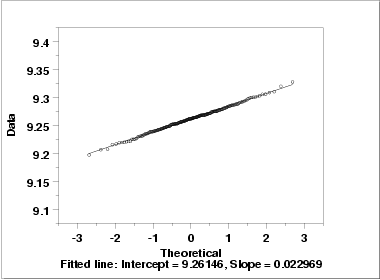
- The normal probability plot (lower right) verifies that an assumption of normality is in fact reasonable.