1.4. EDA Case Studies
1.4.2. Case Studies
1.4.2.1. Normal Random Numbers
1.4.2.1.2. |
Graphical Output and Interpretation |
- Determine if the univariate model:
-
\( Y_{i} = C + E_{i} \)
is appropriate and valid.
- Determine if the typical underlying assumptions for an
"in control" measurement process are valid. These assumptions
are:
- random drawings;
- from a fixed distribution;
- with the distribution having a fixed location; and
- the distribution having a fixed scale.
- Determine if the confidence interval
-
\( \bar{Y} \pm 2s/\sqrt{N} \)
is appropriate and valid where s is the standard deviation of the original data.
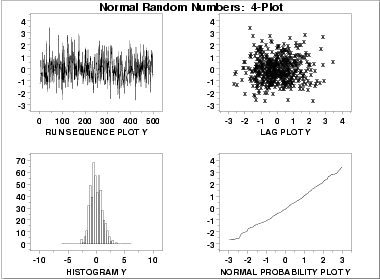
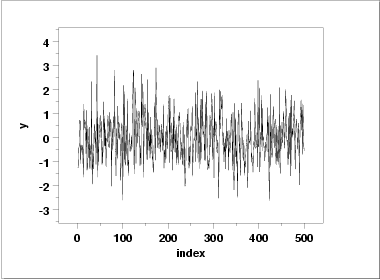
- The run sequence plot
(upper left) indicates that the data do
not have any significant shifts in location or scale over time.
The run sequence plot does not show any obvious outliers.
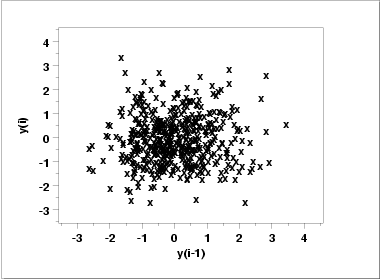
- The lag plot
(upper right) does not indicate any non-random pattern in the
data.
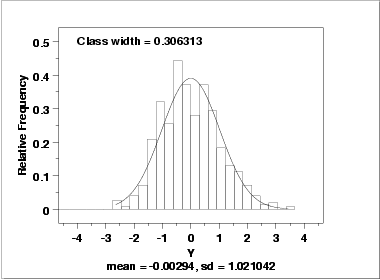
- The histogram (lower left)
shows that the data are reasonably
symmetric, there do not appear to be significant outliers in
the tails, and that it is reasonable to assume that the data are
from approximately a normal distribution.
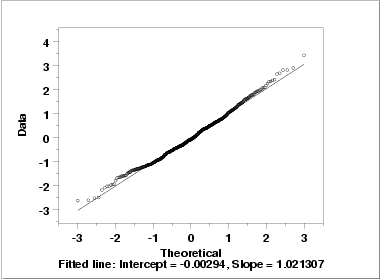
- The normal probability plot (lower right) verifies that an assumption of normality is in fact reasonable.
From the above plots, we conclude that the underlying assumptions are valid and the data follow approximately a normal distribution. Therefore, the confidence interval form given previously is appropriate for quantifying the uncertainty of the population mean. The numerical values for this model are given in the Quantitative Output and Interpretation section.