SPEARMAN DISSIMILARITY

SPEARMAN DISSIMILARITY (LET)
SPEARMAN SIMILARITY (LET)

Let Subcommand

Compute the Spearman rank correlation coefficient transformed to a dissimilarity measure between two variables.

If the measurements in the two samples are replaced with their ranks (and average ranks in the case of ties) and the Pearson correlation coefficient is computed, the result is the Spearman rho correlation coefficient.

The rank correlation is recommended in the following cases:

1. When the underlying data does not have a meaningful numerical measure, but it can be ranked;

2. When the relationship between the two variables is not linear;

3. When the normality assumption for two variables is not valid.

A perfect linear relationship yields a correlation coefficient of +1 (or -1 for a negative relationship) and no linear relationship yields a correlation coefficient of 0.

In some applications, such as clustering, it can be useful to transform the correlation coefficient to a dissimilarity measure. The transformation used here is

\( d = \frac{1 - r}{2} \)

This converts the correlation coefficient with values between -1 and 1 to a score between 0 and 1. High positive correlation (i.e., very similar) results in a dissimilarity near 0 and high negative correlation (i.e., very dissimilar) results in a dissimilarity near 1.

If a similarity score is preferred, you can use

\( s = 1 - d \)

where d is defined as above.

LET <par> = SPEARMAN DISSIMILARITY <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed Spearman dissimilarity is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET <par> = SPEARMAN SIMILARITY <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed Spearman similarity is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = SPEARMAN DISSIMILARITY Y1 Y2
LET A = SPEARMAN DISSIMILARITY Y1 Y2 SUBSET TAG > 2
LET A = SPEARMAN SIMILARITY Y1 Y2

The two variables must have the same number of elements.

None

SPEARMAN DISTANCE is a synonym for SPEARMAN DISSIMILARITY

RANK CORRELATION	=	Compute Spearman rank correlation coefficient.
PEARSON DISSIMILARITY	=	Compute the dissimilarity of two variables based on Pearson correlation.
CORRELATION	=	Compute the Pearson correlation of two variables.
KENDALL TAU DISSIMILARITY	=	Compute the dissimilarity of two variables based on Kendall's tau correlation.
COSINE DISTANCE	=	Compute the cosine distance.
MANHATTAN DISTANCE	=	Compute the Euclidean distance.
EUCLIDEAN DISTANCE	=	Compute the Euclidean distance.
MATRIX DISTANCE	=	Compute various distance metrics for a matrix.
GENERATE MATRIX <stat>	=	Compute a matrix of pairwise statistic values.

Kaufman and Rousseeuw (1990), "Finding Groups in Data: An Introduction To Cluster Analysis", Wiley.

Clustering

2017/08:
2018/10: SPEARMAN DISTANCE is a synonym for SPEARMAN DISSIMILARITY

 
SKIP 25
READ BERGER1.DAT Y X
LET CORR = RANK CORRELATION Y X
LET D    = SPEARMAN DISSIMILARITY Y X
SET WRITE DECIMALS 4
PRINT CORR D
    

The following output is generated

 PARAMETERS AND CONSTANTS--

    CORR    --         0.9486
    D       --         0.0257
    

 
SKIP 25
READ IRIS.DAT Y1 Y2 Y3 Y4
SET WRITE DECIMALS 3
.
LET M = GENERATE MATRIX SPEARMAN DISSIMILARITY Y1 Y2 Y3 Y4
PRINT M
    

The following output is generated

        MATRIX M       --            4 ROWS
                       --            4 COLUMNS

 VARIABLES--M1             M2             M3             M4      

          0.000          0.583          0.059          0.131
          0.583          0.000          0.655          0.506
          0.059          0.655         -0.000          0.084
          0.131          0.506          0.084         -0.000
    

 
SKIP 25
READ IRIS.DAT Y1 Y2 Y3 Y4 TAG
.
TITLE CASE ASIS
TITLE OFFSET 2
CASE ASIS
TIC MARK OFFSET UNITS DATA
YLIMITS 0 1
MAJOR YTIC MARK NUMBER 6
MINOR YTIC MARK NUMBER 1
Y1TIC MARK LABEL DECIMAL 1
XLIMITS 1 3
MAJOR XTIC MARK NUMBER 3
MINOR XTIC MARK NUMBER 0
XTIC MARK OFFSET 0.3 0.3
CHARACTER X BLANK
LINES BLANK SOLID
.
MULTIPLOT CORNER COORDINATES 5 5 95 95
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 3
.
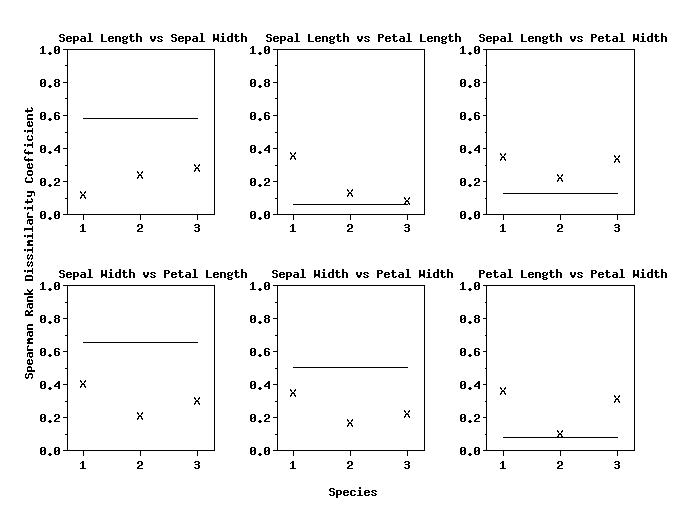
TITLE Sepal Length vs Sepal Width
SPEARMAN DISSIMILARITY PLOT Y1 Y2 TAG
.
TITLE Sepal Length vs Petal Length
SPEARMAN DISSIMILARITY PLOT Y1 Y3 TAG
.
TITLE Sepal Length vs Petal Width
SPEARMAN DISSIMILARITY PLOT Y1 Y4 TAG
.
TITLE Sepal Width vs Petal Length
SPEARMAN DISSIMILARITY PLOT Y2 Y3 TAG
.
TITLE Sepal Width vs Petal Width
SPEARMAN DISSIMILARITY PLOT Y2 Y4 TAG
.
TITLE Petal Length vs Petal Width
SPEARMAN DISSIMILARITY PLOT Y3 Y4 TAG
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 5
TEXT Species
DIRECTION VERTICAL
MOVE 5 50
TEXT Spearman Rank Dissimilarity Coefficient
DIRECTION HORIZONTAL