KAPPPF

KAPPPF (LET)

Library Function

Compute the kappa percent point function with shape parameters h and k.

The general form of the kappa distribution has the following percent point function:
\( G(p;k,h,\xi,\alpha) = \xi + \frac{\alpha}{k} \left( 1 - \left( \frac{1 - p^{h}} {h} \right) ^k \right) \hspace{20pt} 0 < p < 1; \alpha > 0 \)

with k and h denoting the shape parameters and \( \xi \) and \( \alpha \) denoting the location and scale parameters, respectively.

The standard form of the distribution is defined as \( \xi \) = 0 and \( \alpha \) = 1.

LET <y> = KAPPPF(<p>,<k>,<h>,<xi>,<alpha>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable in the range (0,1);
            <k> is a number, parameter, or variable that specifies the first shape parameter;
            <h> is a number, parameter, or variable that specifies the second shape parameter;
            <xi> is a number, parameter, or variable that specifies the location parameter;
            <alpha> is a number, parameter, or variable that specifies the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed kappa ppf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The <xi> and <alpha> parameters are optional.

LET A = KAPPPF(0.95,0.5,2,0,1.5)
LET X2 = KAPPPF(P1,K,H)

Dataplot uses Hoskings QUAKAP routine to compute the kappa percent point function. Hoskings report and associated Fortran code can be downloaded from the Statlib archive at
http://lib.stat.cmu.edu/general/lmoments

None

None

KAPCDF	= Compute the kappa cumulative distribution function.
KAPDPF	= Compute the kappa probability density function.
MIEPDF	= Compute Miekle's beta-kappa probability density function.
GEVPDF	= Compute the generalized extreme value probability density function.
GEPPDF	= Compute the generalized Pareto probability density function.
GL5PDF	= Compute the Hosking's generalized logistic probability density function.

Hosking and Wallis (1997), "Regional Frequency Analysis", Cambridge University Press, Appendix A10.

J. R. M. Hosking (2000), "Research Report: Fortran Routines for use with the Method of L-Moments", IBM Research Division, T. J. Watson Research Center, Yorktown Heights, NY 10598.

Hoskings (1990), "L-moments: Analysis and Estimation of Distribution using Linear Combinations of Order Statistics", Journal of the Royal Statistical Society, Series B, 52, pp. 105-124.

Distributional Modeling

2008/5

 
LET KP = DATA -0.5  0.1  0.5  1.0
LET H1 = -0.5
LET H2 = 0.1
LET H3 = 1
LET H4 = 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 95 95
MULTIPLOT SCALE FACTOR 2
TITLE CASE ASIS
TITLE OFFSET 2
X3LABEL
LINE COLOR BLACK RED BLUE GREEN
.
LOOP FOR KK = 1 1 4
   LET K = KP(KK)
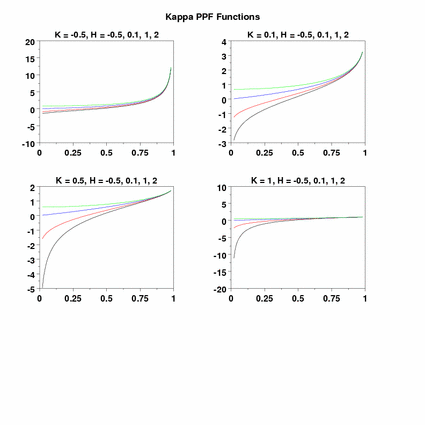
   TITLE K = ^K, H = -0.5, 0.1, 1, 2
   PLOT KAPPPF(P,K,H1) FOR P = 0.02  0.01  0.98  AND
   PLOT KAPPPF(P,K,H2) FOR P = 0.02  0.01  0.98  AND
   PLOT KAPPPF(P,K,H3) FOR P = 0.02  0.01  0.98  AND
   PLOT KAPPPF(P,K,H4) FOR P = 0.02  0.01  0.98
END OF LOOP
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Kappa PPF Functions