INTERPOLATION

INTERPOLATION (LET)

Let Subcommand

Perform a cubic spline interpolation of a series of data points.

Interpolation takes a series of (x,y) points and generates estimated values for y's at new x points. Interpolation is used when the function that generated the original (x,y) points is unknown.

Interpolation is related to, but distinct from, fitting a function to a series of points. In particular, an interpolated function goes through all the original points while a fitted function does not.

There are various methods for performing interpolation. Chapter 3 of the Numerical Recipes book (see REFERENCE below) contains a nice discussion of various types of commonly used interpolation schemes (polynomial interpolation, rational function interpolation, cubic spline interpolation). Dataplot uses the cubic spline algorithm. Cubic splines have the advantage of being efficient to compute and being more stable than polynomials.

Cubic spline interpolation is intended for the case when your data are "smooth". Specifically, it should be monotonically increasing (or decreasing) and not be "noisy". If your data is sufficiently noisy, cubic spline interpolation may not generate desirable interpolated values (e.g., it may not preserve the monotonicity).

Hermite interpolation is an alternative to cubic spline interpolation that may work better when there is some noise in the data (although it still assumes monotonicity). Chapter 4 of Kahaner, Moler, and Nash gives a discussion of Hermite interpolation.

Hermite interpolation also returns the derivative at the interpolated points. You can also compute a definite integral based on the Hermite interpolation.

LET <y2> = INTERPOLATION <y1> <x1> <x2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is a variable containing the vertical axis data points;
            <x1> is a variable containing the horizontal axis data points;
            <x2> is a variable containing the horizontal points where the interpolation is to be performed;
            <y2> is a variable (same length as <x2>) where the interpolated values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the cubic spline interpolation.

LET <y2> = HERMITE INTERPOLATION <y1> <x1> <x2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is a variable containing the vertical axis data points;
            <x1> is a variable containing the horizontal axis data points;
            <x2> is a variable containing the horizontal points where the interpolation is to be performed;
            <y2> is a variable (same length as <x2>) where the interpolated values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the Hermite interpolation.

LET <y2> = HERMITE DERIVATIVE <y1> <x1> <x2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is a variable containing the vertical axis data points;
            <x1> is a variable containing the horizontal axis data points;
            <x2> is a variable containing the horizontal points where the interpolation is to be performed;
            <y2> is a variable (same length as <x2>) where the derivative of the interpolated values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the derivative at the <x2> points based on the Hermite interpolation.

LET <a> = HERMITE INTEGRATION <y1> <x1> <lowlim> <upplim>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is a variable containing the vertical axis data points;
            <x1> is a variable containing the horizontal axis data points;
            <lowlim> is a number or parameter containing the lower limit of the integration;
            <upplim> is a number or parameter containing the upper limit of the integration;
            <a> is a parameter where the integral value is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the definite integral based on the Hermite interpolation.

LET Y2 = INTERPOLATION Y1 X1 X2
LET Y2 = HERMITE INTERPOLATION Y1 X1 X2


LET Y2 = HERMITE DERIVATIVE Y1 X1 X2


LET A = HERMITE INTEGRATION Y1 X1 0 1

The interpolation points (i.e., <x2>) must be within the range of the original data points (i.e., <x1>). An error message is generated if this is not the case.

The original data do not have to be in sorted order. DATAPLOT sorts the original data (on <x1>) automatically.

Dataplot implements Hermite interpolation and integration using the PCHEV routinge from Kahaner, Moler, and Nash. PCHEV is a calling routine for the PCHIP package developed by Fritsch and Carlson.

None

HERMITE INTEGRAL is a synonym for HERMITE INTEGRATION.

LINEAR INTERPOLATION	=	Compute a linear interpolation of a series of points.
BILINEAR INTERPOLATION	=	Compute a bi-linear interpolation of a gridded 2d series of points.
BIVARIATE INTERPOLATION	=	Compute an interpolation of a gridded 2d series of points.
2D INTERPOLATION	=	Compute an interpolation of a irregular 2d series of points to a grid.
FIT	=	Perform a least squares fit.
ROOTS	=	Compute the roots of a function.
INTEGRAL	=	Compute the integral of a function.
DERIVATIVE	=	Compute the derivative of a function.
SEQUENCE	=	Generate a sequence of numbers.

Ralston and Rubinowitz (1978), "A First Course in Numerical Analysis", McGraw-Hill.

Press, Flannery, Teukolsky, and Vetterling (1989), "Numerical Recipes: The Art of Scientific Computing (FORTRAN Version)", Cambridge University Press, (chapter 3).

Kahaner, Moler, and Nash (1989), "Numerical Methods and Software", Prentice-Hall, chapter 4.

Fritsch and Carlson (1980), "Monotone Piecewise Cubic Interpolation", SIAM Journal of Numerical Analysis, Vol. 17, No. 2, pp. 238-246).

Fritsch and Carlson (1982), "Piecewise Cubic Hermite Interpolation Package, Final Specifications", Lawrence Livermore National Laboratory, Computer Documentation UCID-30194.

Mathematics

Pre-1987
2017/09: Support for Hermite interpolation and integration
2017/11: Support for Hermite derivative

 
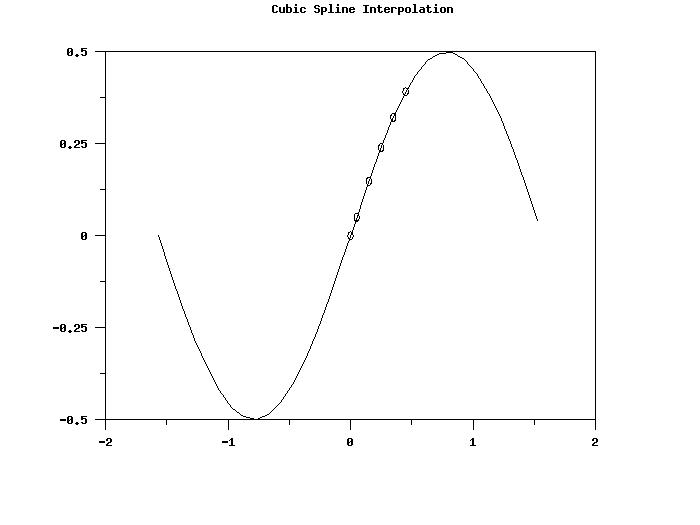
LET FUNCTION F1 = SIN(X1)*COS(X1)
LET START = -PI/2
LET STOP = PI/2
LET X1 = SEQUENCE START 0.1 STOP
LET Y1 = F1
LET X2 = DATA 0 0.05 0.15 0.25 0.35 0.45
.
LET Y2 = INTERPOLATION Y1 X1 X2
.
TITLE CASE ASIS
LINES SOLID BLANK
CHARACTER BLANK CIRCLE
CHARACTER SIZE 1.5 ALL
CHARACTER FILL OFF ON
TITLE Cubic Spline Interpolation
PLOT Y1 X1 AND
PLOT Y2 X2
.
LET Y3 = HERMITE INTERPOLATION Y1 X1 X2
.
TITLE Hermite Cubic Interpolation
PLOT Y1 X1 AND
PLOT Y3 X2