GLDCDF

GLDCDF (LET)

Library Function

Compute the generalized Tukey-Lambda cumulative distribution function.

The generalized Tukey-Lambda distribution is defined in terms of its percent point function. Note that there are two parameterizations of this distribution in the literature.

The original parameterization, referred to as the RS generalized Tukey-Lambda distribution, given by Ramberg and Schmeiser has the percent point function

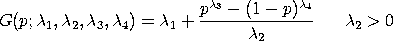
with , , , and denoting the location, the scale, and the two shape parameters, respectively.

One drawback of this parameterization is that it does not define a valid probability distribution for certain values of the parameters. Futhermore, the regions that do not define a valid probability distribution are not simple. For this reason, Friemer, Mudholkar, Kollia, and Lin developed an alternative parameterization, referred to as the FMLKL generalized Tukey-Lambda distribution, that has the percent point function

with , , , and denoting the location, the scale, and the two shape parameters, respectively.

Note that = 0 or = 0 results in division by zero in the above formula.

If = 0, then

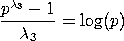
Likewise, if = 0, then

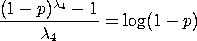
The advantage of the FMKL parameterization is that it defines a valid probability distribution for all real values of and . For this reason, Dataplot uses the FMKL parameterization.

The generalized Tukey-Lambda cumulative distribution function is computed by numerically inverting the percent point function.

A few relevant properties for this distribution are:

1. If = , then the generalized Tukey-Lambda distribution reduces to the symmetric Tukey-Lambda distribution.

2. The parameter controls the behavior of the lower tail. If > 0, then the distribution is bounded below at -1/. If ≤ 0, then the distribution is unbounded below.

3. The parameter controls the behavior of the upper tail. If > 0, then the distribution is bounded above at 1/. If ≤ 0, then the distribution is unbounded above.

4. The kth moment is finite only if min(, ) > -1/k. So this distribution has finite mean only if min(, ) > -1 and finite variance only if min(, ) > -0.5.

LET <y> = GLDCDF(<x>,<l3>,<l4>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number, or parameter;
            <l3> is a number or parameter that specifies the first shape parameter;
            <l4> is a number or parameter that specifies the second shape parameter;
            <loc> is a number or parameter that specifies the location parameter;
            <scale> is a number or parameter that specifies the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized Tukey-Lambda cdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Note that the location and scale parameters are optional.

LET A = GLDCDF(0.9,0.5,0.2)
LET Y = GLDCDF(X,0.5,0.2)
PLOT GLDCDF(X,0.5,0.2) FOR X = -2 0.01 5

None

None

GLDPDF	= Compute the generalized Tukey-Lambda probability density function.
GLDPPF	= Compute the generalized Tukey-Lambda percent point function.
LAMPPF	= Compute the Tukey-Lambda probability density function.
GHPPF	= Compute the g-and-h probability density function.
JSUPPF	= Compute the Johnson SU probability density function.
JSBPPF	= Compute the Johnson SB probability density function.
PPCC PLOT	= Generate a ppcc plot.
PROBABILITY PLOT	= Generate a probability plot.

Ramberg and Schmeiser (1972), "An Approximate Method for Generating Symmetric Random Variables", Communications of the Association for Computing Machinery, 15, pp. 987-990.

Ramberg and Schmeiser (1974), "An Approximate Method for Generating Asymmetric Random Variables", Communications of the Association for Computing Machinery, 17, pp. 78-82.

Ozturk and Dale (1985), "Least Squares Estimation of the Parameters of the Generalized Lambda Distribution", Technometrics, Vol. 27, No. 1, pp. 81-84.

Friemer, Mudholkar, Kollia, and Lin (1988), "A Study of the Generalized Lambda Family", Communications in Statistics-Theory and Methods, 17, pp. 3547-3567.

King and MacGillivray (1999), "A Starship Estimation Method for the Generalized Lambda Distributions", Australia and New Zealand Journal of Statistics, 41(3), pp. 353-374.

Karian and Dudewicz (2000), Fitting Statistical Distributions: The Generalized Bootstrap Methods, New York, Chapman & Hall.

Su (2005), "A Discretized Approach to Flexibly Fit Generalized Lambda Distributions to Data", Journal of Modern Applied Statistical Methods, Vol. 4, No. 2, pp. 408-424.

Distributional Modeling

2006/3

 
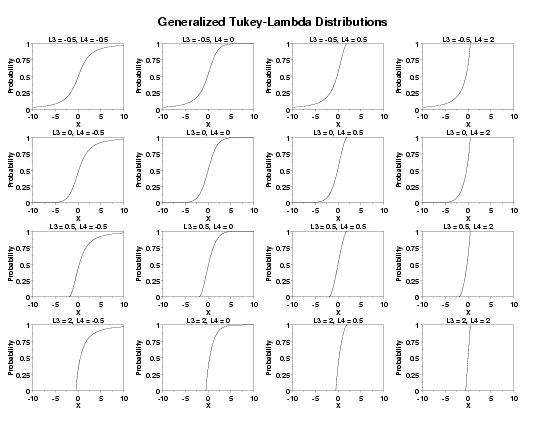
MULTIPLOT 4 4
MULTIPLOT SCALE FACTOR 2.5
MULTIPLOT CORNER COORDINATES 0 0 100 95
LABEL CASE ASIS
X1LABEL X
Y1LABEL Probability
X1LABEL DISPLACEMENT 16
Y1LABEL DISPLACEMENT 18
TITLE DISPLACEMENT 2
XLIMITS -10 10
LET LAMBDA3 = DATA -0.5 0 0.5 2
LET LAMBDA4 = DATA -0.5 0 0.5 2
LOOP FOR K = 1 1 4
    LET L3 = LAMBDA3(K)
    LET XLOW = -10
    IF L3 > 0
       LET XLOW = -1/L3
    END OF IF
    LOOP FOR L = 1 1 4
        LET L4 = LAMBDA4(L)
        LET XUPP = 10
        IF L4 > 0
           LET XUPP = 1/L4
        END OF IF
        TITLE L3 = ^L3, L4 = ^L4
        PLOT GLDCDF(X,L3,L4) FOR X = XLOW  0.01  XUPP
    END OF LOOP
END OF LOOP
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
CASE ASIS
TEXT Generalized Tukey-Lambda Distributions