

|
JSBPPFName:
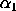 and and
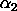 . .
![f(x) = [alpha2/(X*(1-X)]*NORPDF(ALPHA1 + ALPHA2*LOG(X/(1-X))
0 < x < 1; alpha2 > 0](eqns/jsbpdf.gif)
where The Johnson SB percent point function does not exist in simple closed form. It is computed numerically using a bisection method.
where <p> is a number, parameter, or variable containing values between 0 and 1; <y> is a variable or a parameter (depending on what <x> is) where the computed Johnson SB ppf values are stored; <alpha1> is a number, parameter, or variable that specifies the first shape parameter; <alpha2> is a number, parameter, or variable that specifies the second shape parameter; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
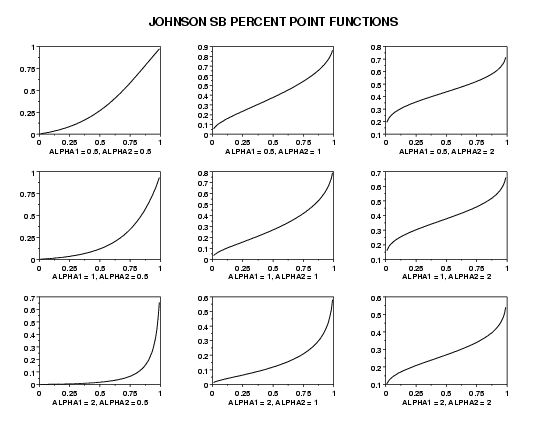
LET A = JSBPPF(P1,1.5,3) LET Y = JSBPPF(P,2,6) PLOT JSBPPF(P,0.8,2) FOR P = 0.01 0.01 0.99
LET ALPHA1 = DATA 0.5 0.5 0.5 1 1 1 2 2 2
LET ALPHA2 = DATA 0.5 1 2 0.5 1 2 0.5 1 2
.
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
LOOP FOR K = 1 1 9
LET A1 = ALPHA1(K)
LET A2 = ALPHA2(K)
X1LABEL ALPHA1 = ^A1, ALPHA2 = ^A2
PLOT JSBPPF(P,A1,A2) FOR P = 0.01 0.01 0.99
END OF LOOP
END OF MULTIPLOT
.
MOVE 50 97
HEIGHT 3
JUSTIFICATION CENTER
TEXT JOHNSON SB PERCENT POINT FUNCTIONS
Date created: 11/20/2001 |