

|
AAD TO MEDIANName:
where AAD and \( \tilde{x} \) denote the average absolute deviation and the median, respectively. This is the statistic computed by this command. Note that the AAD used here is defined as
That is, we compute the deviations from the median rather than the mean. This statistic is a robust alternative to the coefficient of variation.
<SUBSET/EXCEPT/FOR qualification> where <y> is a response variable; <par> is a parameter where the AAD TO MEDIAN value is saved; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; <par> is a parameter where the AAD TO MEDIAN value is saved; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET D = AAD TO MEDIAN Y1 SUBSET TAG > 2
LET D = DIFFERENCE OF AAD TO MEDIAN Y1
LET Y1 = DOUBLE EXPONENTIAL NUMBERS FOR I = 1 1 100
LET D = AAD TO MEDIAN Y1
Program 2:
. Step 1: Create the data
.
skip 25
read gear.dat y x
skip 0
set write decimals 6
.
. Step 2: Define plot control
.
title case asis
title offset 2
label case asis
.
y1label Coefficient of Dispersion (AAD to Median)
x1label Group
title AAD to Median for GEAR.DAT
let ngroup = unique x
xlimits 1 ngroup
major x1tic mark number ngroup
minor x1tic mark number 0
tic mark offset units data
x1tic mark offset 0.5 0.5
y1tic mark label decimals 3
.
character X
line blank
.
set statistic plot reference line average
aad to median plot y x
.
tabulate aad to median y x
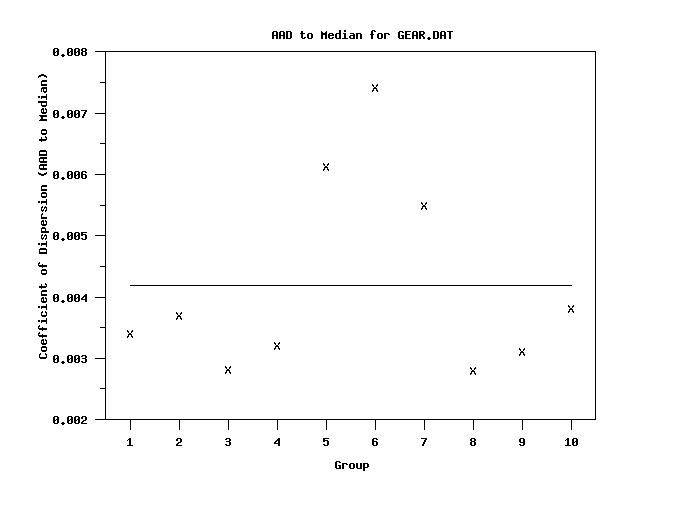
Cross Tabulate AAD TO MEDIAN
(Response Variables: Y )
---------------------------------------------
X | AAD TO MEDIAN
---------------------------------------------
1.000000 | 0.003405
2.000000 | 0.003704
3.000000 | 0.002811
4.000000 | 0.003210
5.000000 | 0.006134
6.000000 | 0.007419
7.000000 | 0.005497
8.000000 | 0.002800
9.000000 | 0.003106
10.000000 | 0.003815
Program 3:
SKIP 25 READ IRIS.DAT Y1 TO Y4 X . LET A = DIFFERENCE OF AAD TO MEDIAN Y1 Y2 SET WRITE DECIMALS 4 TABULATE DIFFERENCE OF AAD TO MEDIAN Y1 Y2 X 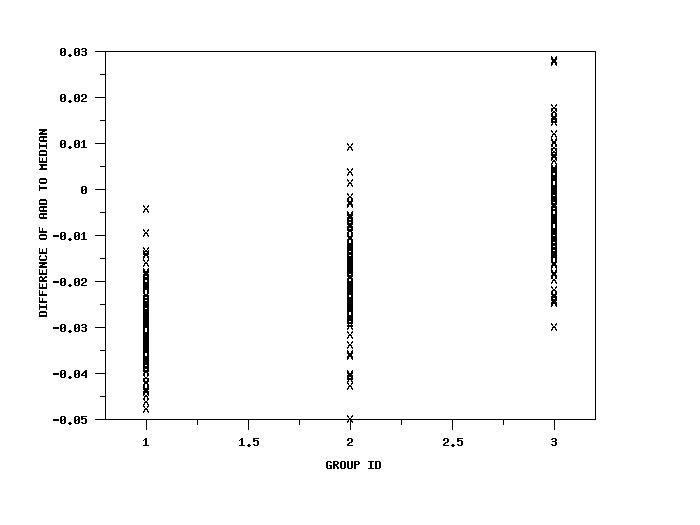
|
Privacy
Policy/Security Notice
NIST is an agency of the U.S.
Commerce Department.
Date created: 01/24/2017 | ||||||||||||||||||||||||||||