5. Process Improvement
5.4. Analysis of DOE data
5.4.7. Examples of DOE's

5.4.7.3.

Response surface model example

Data Source

A CCD with two responses

This example uses experimental data published in Czitrom and Spagon, (1997), Statistical Case Studies for Industrial Process Improvement. The material is copyrighted by the American Statistical Association and the Society for Industrial and Applied Mathematics, and is used with their permission. Specifically, Chapter 15, titled "Elimination of TiN Peeling During Exposure to CVD Tungsten Deposition Process Using Designed Experiments", describes a semiconductor wafer processing experiment (labeled Experiment 2).

Goal, response variables, and factor variables

The goal of this experiment was to fit response surface models to the two responses, deposition layer Uniformity and deposition layer Stress, as a function of two particular controllable factors of the chemical vapor deposition (CVD) reactor process. These factors were Pressure (measured in torr) and the ratio of the gaseous reactants H₂ and WF₆ (called H₂/WF₆). The experiment also included an important third (categorical) response - the presence or absence of titanium nitride (TiN) peeling. The third response has been omitted in this example in order to focus on the response surface aspects of the experiment.

To summarize, the goal is to obtain a response surface model for two responses, Uniformity and Stress. The factors are: Pressure and H₂/WF₆.

Experiment Description

The design is a 13-run CCI design with 3 centerpoints

The minimum and maximum values chosen for Pressure were 4 torr and 80 torr (0.5333 kPa and 10.6658 kPa). Although the international system of units indicates that the standard unit for pressure is Pascal, or 1 N/m², we use torr to be consistent with the analysis appearing in the paper by Czitrom and Spagon.

The minimum and maximum H₂/WF₆ ratios were chosen to be 2 and 10. Since response curvature, especially for Uniformity, was a distinct possibility, an experimental design that allowed estimating a second order (quadratic) model was needed. The experimenters decided to use a central composite inscribed (CCI) design. For two factors, this design is typically recommended to have 13 runs with 5 centerpoint runs. However, the experimenters, perhaps to conserve a limited supply of wafer resources, chose to include only 3 centerpoint runs. The design is still rotatable, but the uniform precision property has been sacrificed.

Table containing the CCI design points and experimental responses

The table below shows the CCI design and experimental responses, in the order in which they were run (presumably randomized). The last two columns show coded values of the factors. (The reader can download the data as a text file.)

Run	Pressure	H2/WF6	Uniformity	Stress	Coded Pressure	Coded H2/WF6
1	80	6	4.6	8.04	1	0
2	42	6	6.2	7.78	0	0
3	68.87	3.17	3.4	7.58	0.71	-0.71
4	15.13	8.83	6.9	7.27	-0.71	0.71
5	4	6	7.3	6.49	-1	0
6	42	6	6.4	7.69	0	0
7	15.13	3.17	8.6	6.66	-0.71	-0.71
8	42	2	6.3	7.16	0	-1
9	68.87	8.83	5.1	8.33	0.71	0.71
10	42	10	5.4	8.19	0	1
11	42	6	5.0	7.90	0	0

Low values of both responses are better than high

Uniformity is calculated from four-point probe sheet resistance measurements made at 49 different locations across a wafer. The value in the table is the standard deviation of the 49 measurements divided by their mean, expressed as a percentage. So a smaller value of Uniformity indicates a more uniform layer - hence, lower values are desirable. The Stress calculation is based on an optical measurement of wafer bow, and again lower values are more desirable.

Analysis of DOE Data

The analyses shown in this page can be generated using R code.

Steps for fitting a response surface model

The steps for fitting a response surface (second-order or quadratic) model are as follows:

1. Fit the full model to the first response.
2. Use stepwise regression, forward selection, or backward elimination to identify important variables.
3. When selecting variables for inclusion in the model, follow the hierarchy principle and keep all main effects that are part of significant higher-order terms or interactions, even if the main effect p-value is larger than you would like (note that not all analysts agree with this principle).
4. Generate diagnostic residual plots (histograms, box plots, normal plots, etc.) for the model selected.
5. Examine the fitted model plot, interaction plots, and ANOVA statistics (R², adjusted R², lack-of-fit test, etc.). Use all these plots and statistics to determine whether the model fit is satisfactory.
6. Use contour plots of the response surface to explore the effect of changing factor levels on the response.
7. Repeat all the above steps for the second response variable.
8. After satisfactory models have been fit to both responses, you can overlay the surface contours for both responses.
9. Find optimal factor settings.

Fitting a Model to the Uniformity Response, Simplifying the Model and Checking Residuals

Fit full quadratic model to Uniformity response

Source              Estimate  Std. Error  t value  Pr(>|t|)   
------              --------  ----------  -------  --------
Intercept            5.86613     0.41773   14.043  3.29e-05
Pressure            -1.90967     0.36103   -5.289  0.00322 
H2/WF6              -0.22408     0.36103   -0.621  0.56201   
Pressure*H2/WF6      1.68617     0.71766    2.350  0.06560
Pressure^2           0.13373     0.60733    0.220  0.83442
H2/WF6^2             0.03373     0.60733    0.056  0.95786


Residual standard error:  0.7235 based on 5 degrees of freedom
Multiple R-squared:  0.8716
Adjusted R-squared:  0.7431 
F-statistic:  6.787 based on 5 and 5 degrees of freedom
p-value:  0.0278

Stepwise regression for Uniformity

Start:   AIC=-3.79
Model:   Uniformity ~ Pressure + H2/WF6 + Pressure*H2/WF6 + Pressure^2 + H2/WF6^2

Step 1:  Remove H2/WF6^2, AIC=-5.79
Model:   Uniformity ~ Pressure + H2/WF6 + Pressure*H2/WF6 + Pressure^2 

Step 2:  Remove Pressure^2,  AIC=-7.69
Model:   Uniformity ~ Pressure + H2/WF6 + Pressure*H2/WF6 

Step 3:  Remove H2/WF6,  AIC=-8.88
Model:   Uniformity ~ Pressure + Pressure*H2/WF6 

The stepwise routine selects a model containing the intercept, Pressure, and the interaction term. However, many statisticians do not think an interaction term should be included in a model unless both main effects are also included. Thus, we will use the model from Step 2 that included Pressure, H2/WF6, and the interaction term. Interaction plots confirm the need for an interaction term in the model.

Analysis of model selected by stepwise regression for Uniformity

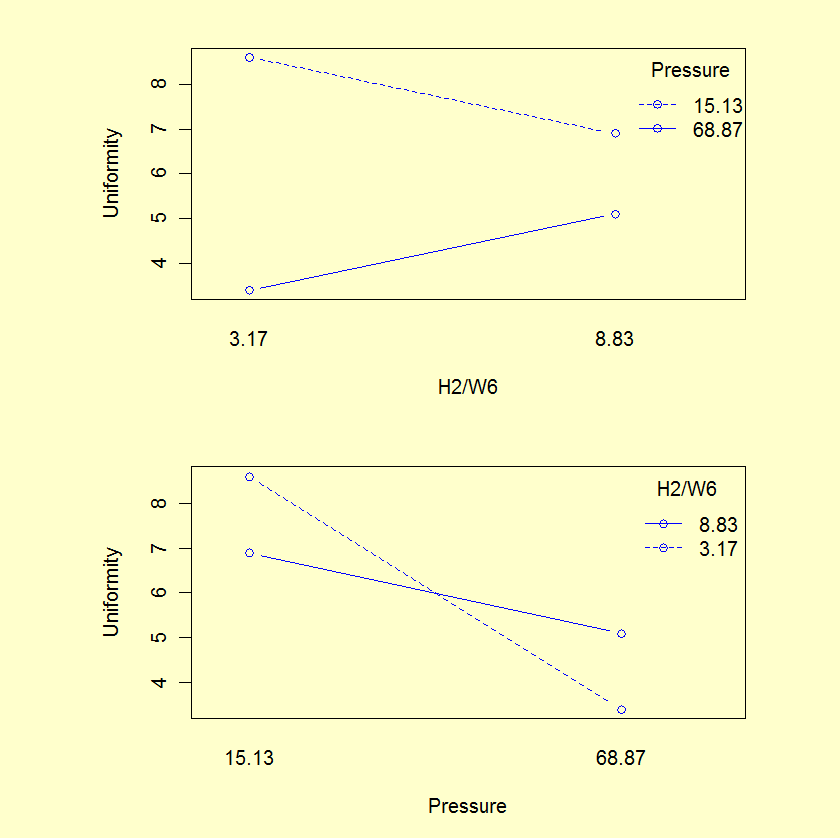
Source           DF Sum of Sq  Mean Sq   F value   Pr(>F)
------           -- ---------  -------   -------   ------
Model             3   17.739   5.9130      15.66   0.0017
Total error       7    2.643   0.3776                      

Lack-of-fit       5   1.4963   0.2993       0.52   0.7588
Pure error        2   1.1467   0.5734


Residual standard error:  0.6145 based on 7 degrees of freedom
Multiple R-squared:  0.8703
Adjusted R-squared:  0.8148 


Source           Estimate  Std. Error  t value  Pr(>|t|)   
------           --------  ----------  -------  -------- 
Intercept          5.9273     0.1853    31.993  7.54e-09
Pressure          -1.9097     0.3066    -6.228  0.000433
H2/WF6            -0.2241     0.3066    -0.731  0.488607   
Pressure*H2/WF6    1.6862     0.6095     2.767  0.027829

A contour plot and perspective plot of Uniformity provide a visual display of the response surface.

Residual plots

We perform a residuals analysis to validate the model assumptions. We generate a normal plot, a box plot, a histogram and a run-order plot of the residuals.

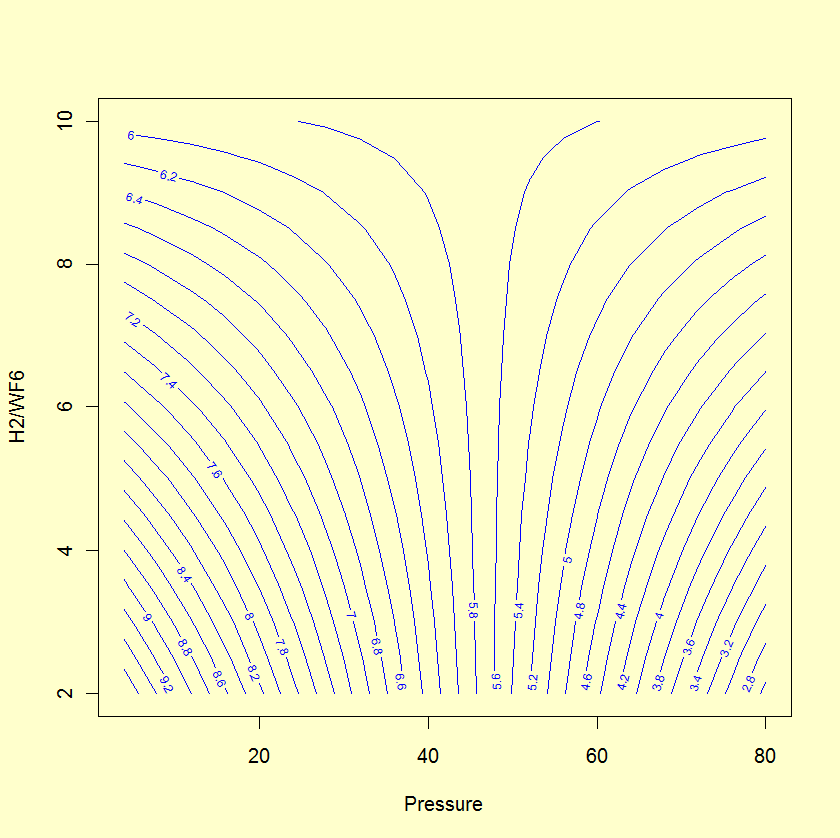
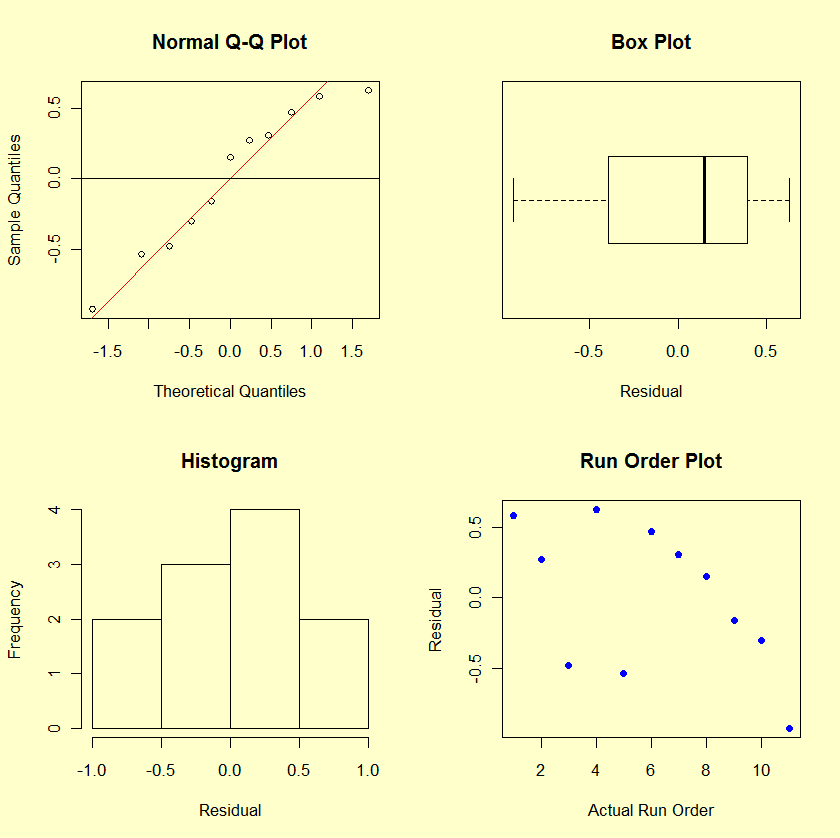
The residual plots do not indicate problems with the underlying assumptions.

Conclusions from the analysis

From the above output, we make the following conclusions.

• The R² is reasonable for fitting Uniformity (well known to be a difficult response to model).
• The lack-of-fit test is not significant (very small "Prob > F " would indicate a lack of fit).
• The residual plots do not reveal any major violations of the underlying assumptions.
• The interaction plot shows why an interaction term is needed (parallel lines would suggest no interaction).

Fitting a Model to the Stress Response, Simplifying the Model and Checking Residuals

Fit full quadratic model to Stress response

Source            Estimate  Std. Error  t value  Pr(>|t|) 
------            --------   ---------  -------  --------
Intercept         8.056791    0.179561   44.869  1.04e-07
Pressure          0.735933    0.038524   19.103  7.25e-06 
H2/WF6            0.852099    0.198192    4.299   0.00772
Pressure*H2/WF6   0.069431    0.076578    0.907   0.40616
Pressure^2       -0.528848    0.064839   -8.156   0.00045
H2/WF6^2         -0.007414    0.004057   -1.827   0.12722 


Residual standard error:  0.07721 based on 5 degrees of freedom
Multiple R-squared:  0.9917
Adjusted R-squared:  0.9834 
F-statistic:  119.8 based on 5 and 5 degrees of freedom
p-value:  3.358e-05 

Stepwise regression for Stress

Start:   AIC=-53.02
Model:   Stress ~ Pressure + H2/WF6 + Pressure*H2/WF6 + Pressure^2 + H2/WF6^2

Step 1:  AIC=-53.35
Model:   Stress ~ Pressure + H2/WF6 + Pressure^2 + H2/WF6^2

The stepwise routine identifies a model containing the intercept, the main effects, and both squared terms. However, the fit of the full quadratic model indicates that neither the H2/WF6 squared term nor the interaction term are significant. A comparison of the full model and the model containing just the main effects and squared pressure terms indicates that there is no significant difference between the two models.

Model 1: Stress ~ Pressure + H2/WF6 + Pressure^2
Model 2: Stress ~ Pressure + H2/WF6 + Pressure^2 + Pressure*H2/WF6 + H2/WF6^2

Source      DF Sum of Sq  Mean Sq   F value    Pr(>F)
------      -- ---------  -------   -------   -------
Model 1      2  0.024802  0.01240      2.08      0.22 
Model 2      5  0.029804  0.00596  

In addition, interaction plots do not indicate any significant interaction. Thus, we will proceed with the model containing main effects and the squared pressure term.

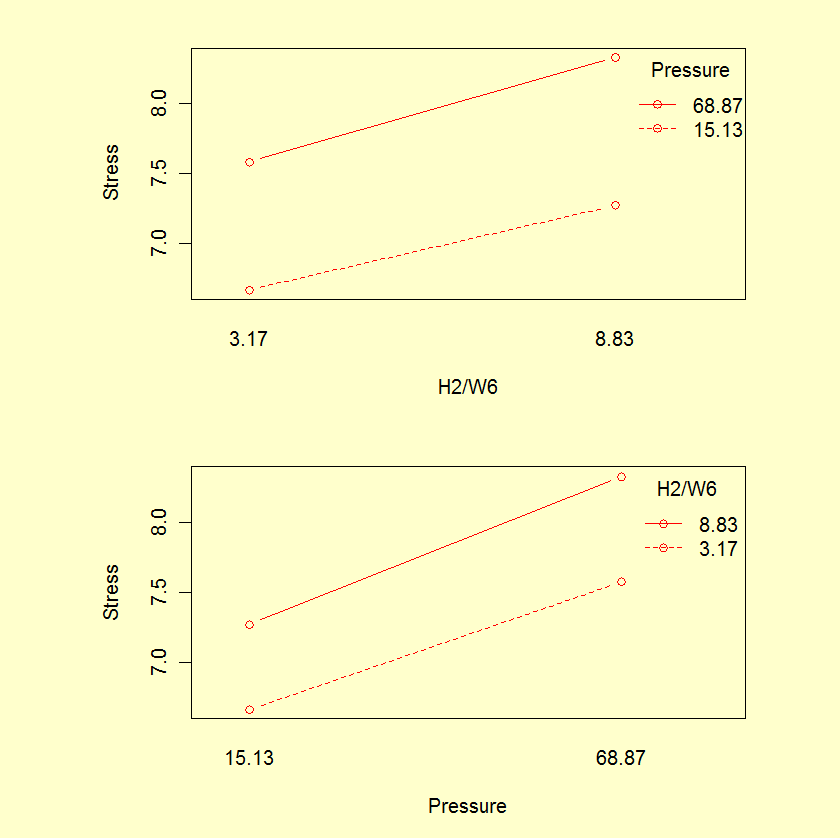
The fact that the stepwise procedure selected a model for Stress containing a term that was not significant indicates that all output generated by statistical software should be carefully examined. In this case, the stepwise procedure identified the model with the lowest AIC (Akaike information criterion), but did not take into account contributions by individual terms. Other software using a different criteria may identify a different model, so it is important to understand the algorithms being used.

Analysis of reduced model for Stress

Source           DF Sum of Sq  Mean Sq   F value    Pr(>F)
------           -- ---------  -------   -------   -------
Model             3    3.5454   1.1818     151.5   9.9e-07 
Total error       7    0.0546   0.0078                       

Lack-of-fit       5  0.032405  0.00065      0.58      0.73
Pure error        2  0.022200  0.01110


Residual standard error:  0.0883 based on 7 degrees of freedom
Multiple R-squared:  0.9848
Adjusted R-squared:  0.9783 


Source        Estimate  Std. Error  t value  Pr(>|t|)    
------        --------  ----------  -------  --------
Intercept      7.73410    0.03715   208.185  1.56e-14
Pressure       0.73593    0.04407    16.699  6.75e-07
H2/WF6         0.49686    0.04407    11.274  9.65e-06
Pressure^2    -0.49426    0.07094    -6.967  0.000218 

A contour plot and perspective plot of Stress provide a visual representation of the response surface.

Residual plots

We perform a residuals analysis to validate the model by generating a run-order plot, box plot, histogram, and normal probability plot of the residuals.

The residual plots do not indicate any major violations of the underlying assumptions.

Conclusions

From the above output, we make the following conclusions.

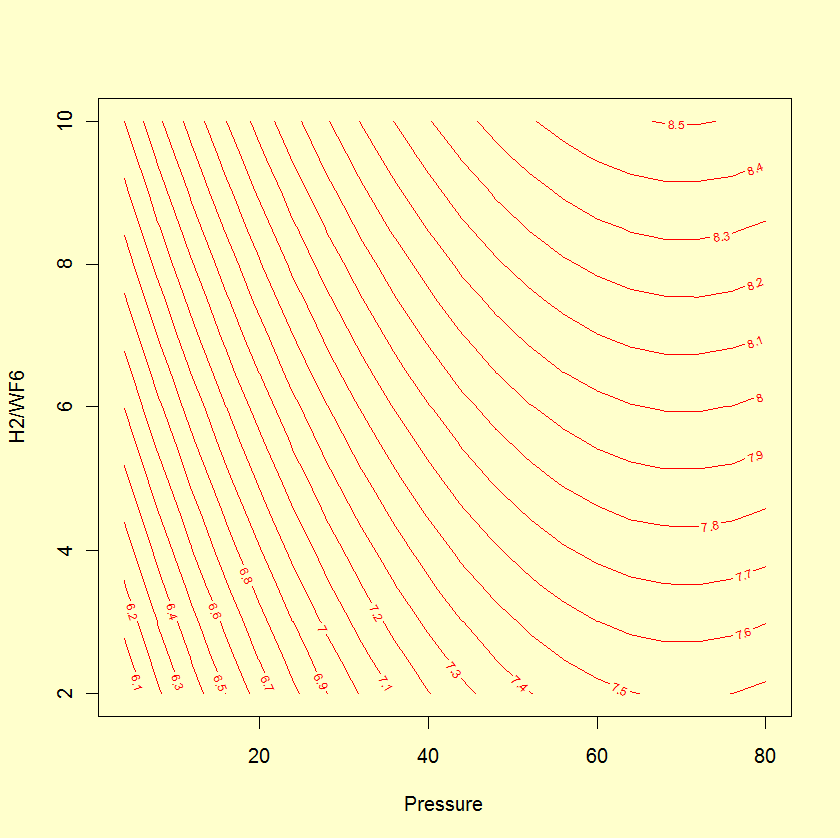
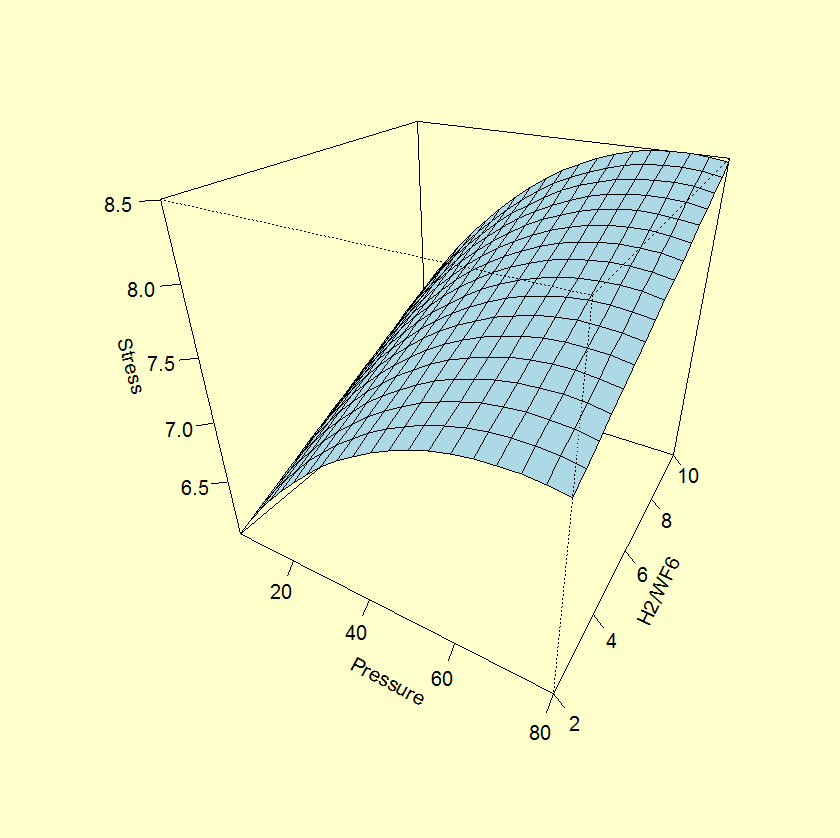
• The R² is very good for fitting Stress.
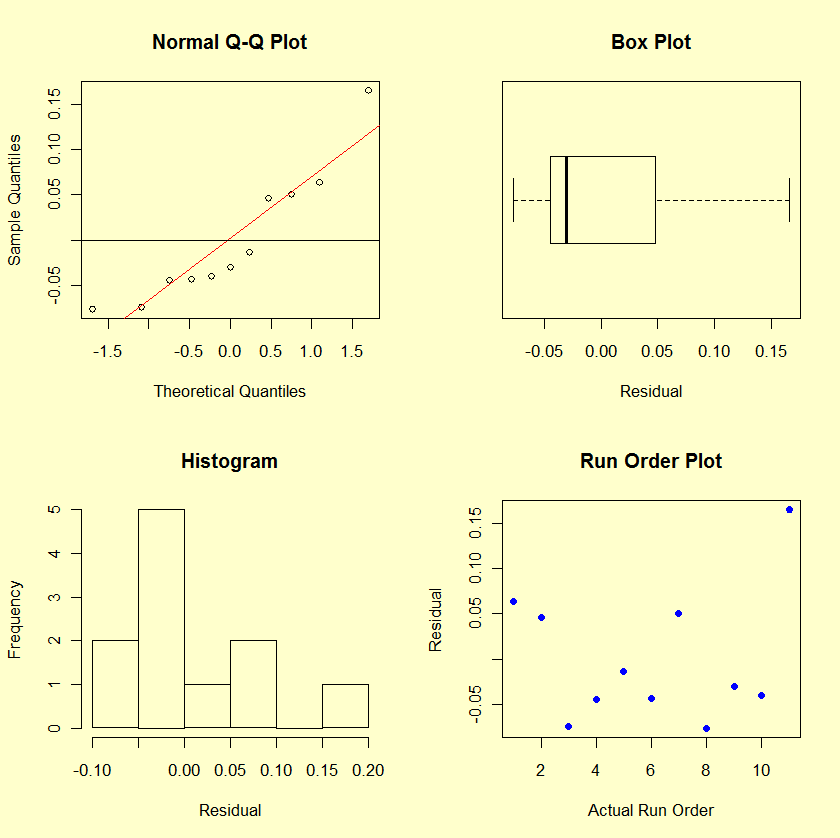
• The lack-of-fit test is not significant (very small "Prob > F " would indicate a lack of fit).
• The residual plots do not reveal any major violations of the underlying assumptions.
• The nearly parallel lines in the interaction plots show why an interaction term is not needed.

Response Surface Contours for Both Responses

Overlay contour plots

We overlay the contour plots for the two responses to visually compare the surfaces over the region of interest.

Summary

Final response surface models

The response surface models fit to (coded) Uniformity and Stress were:

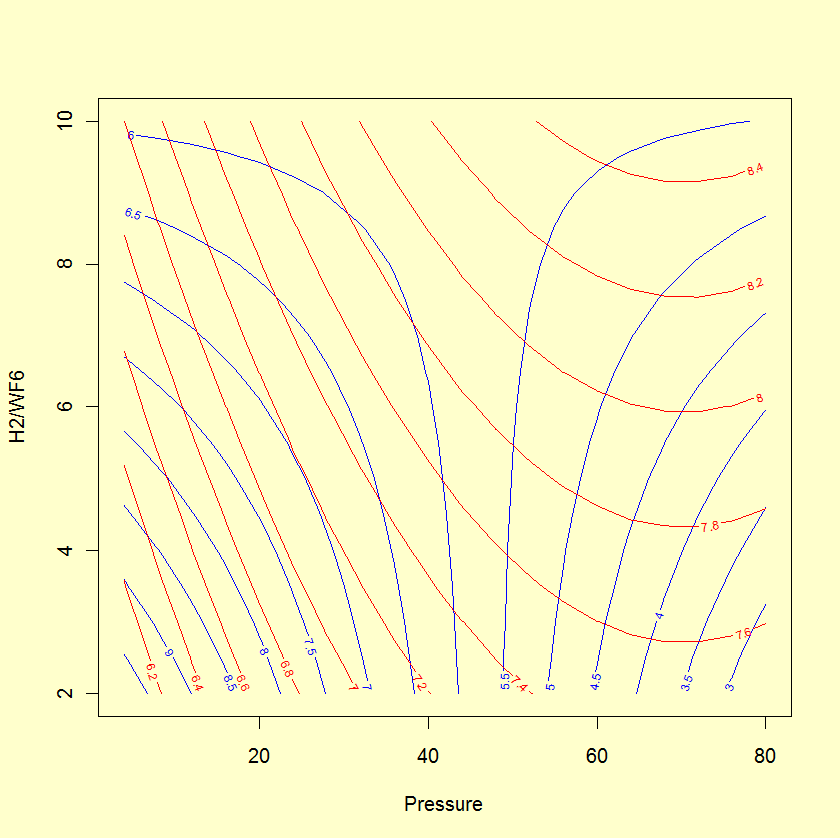
Uniformity = 5.93 - 1.91*Pressure - 0.22*H₂/WF₆ + 1.70*Pressure*H₂/WF₆

Stress = 7.73 + 0.74*Pressure + 0.50*H₂/WF₆ - 0.49*Pressure²

Trade-offs are often needed for multiple responses

The models and the corresponding contour plots show that trade-offs have to be made when trying to achieve low values for both Uniformity and Stress since a high value of Pressure is good for Uniformity while a low value of Pressure is good for Stress. While low values of H₂/WF₆ are good for both responses, the situation is further complicated by the fact that the Peeling response (not considered in this analysis) was unacceptable for values of H₂/WF₆ below approximately 5.

Uniformity was chosen as more important

In this case, the experimenters chose to focus on optimizing Uniformity while keeping H₂/WF₆ at 5. That meant setting Pressure at 80 torr.

Confirmation runs validated the model projections

A set of 16 verification runs at the chosen conditions confirmed that all goals, except those for the Stress response, were met by this set of process settings.