3. Production Process Characterization
3.4. Data Analysis for PPC

3.4.4.

Analyzing Variance Structure

Studying variation is important in PPC

One of the most common activities in process characterization work is to study the variation associated with the process and to try to determine the important sources of that variation. This is called analysis of variance. Refer to the section of this chapter on ANOVA models for a discussion of the theory behind this kind of analysis.

The key is to know the structure

The key to performing an analysis of variance is identifying the structure represented by the data. In the ANOVA models section we discussed one-way layouts and two-way layouts where the factors are either crossed or nested. Review these sections if you want to learn more about ANOVA structural layouts.

To perform the analysis, we just identify the structure, enter the data for each of the factors and levels into a statistical analysis program and then interpret the ANOVA table and other output. This is all illustrated in the example below.

Example: furnace oxide thickness with a 1-way layout

The example is a furnace operation in semiconductor manufacture where we are growing an oxide layer on a wafer. Each lot of wafers is placed on quartz containers (boats) and then placed in a long tube-furnace. They are then raised to a certain temperature and held for a period of time in a gas flow. We want to understand the important factors in this operation. The furnace is broken down into four sections (zones) and two wafers from each lot in each zone are measured for the thickness of the oxide layer.

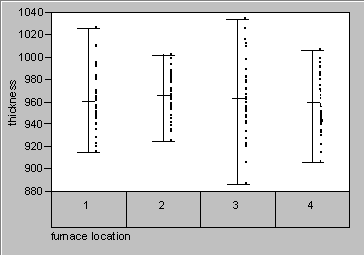
Look at effect of zone location on oxide thickness

The first thing to look at is the effect of zone location on the oxide thickness. This is a classic  one-way layout. The factor is furnace zone and we have four levels. A plot of the data and an ANOVA table are given below.

The zone effect is masked by the lot-to-lot variation

ANOVA table

Analysis of Variance

Source	DF	SS	Mean Square	F Ratio	Prob > F
Zone	3	912.6905	304.23	0.467612	0.70527
Within	164	106699.1	650.604

Let's account for lot with a nested layout

From the graph there does not appear to be much of a zone effect; in fact, the ANOVA table indicates that it is not significant. The problem is that variation due to lots is so large that it is masking the zone effect. We can fix this by adding a factor for lot. By treating this as a nested two-way layout, we obtain the ANOVA table below.

Now both lot and zone are revealed as important

Analysis of Variance

Source	DF	SS	Mean Square	F Ratio	Prob > F
Lot	20	61442.29	3072.11	5.37404	1.39e-7
Zone[lot]	63	36014.5	571.659	4.72864	3.9e-11
Within	84	10155	120.893

Conclusions

Since the "Prob > F" is less than 0.05, for both lot and zone, we know that these factors are statistically significant at the 0.05 significance level.