6. Process or Product Monitoring and Control
6.3. Univariate and Multivariate Control Charts
6.3.3. What are Multivariate Control Charts?

6.3.3.3.

Multivariate EWMA Charts

Multivariate EWMA Control Chart 

The model for a univariate EWMA  chart is given by: 

       and  0 < l  .£  1. 

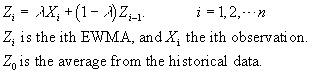
In the multivariate case, one can extend this formula to 

The following illustration may clarify this. There are p variables and each variable contains n observations. The input data matrix looks like: The quantity to be plotted on the control chart is     There is a further simplification. If i becomes large the covariance matrix may be expressed as:  The question is "What is large?".  When we examine the formula with the 2i  in it, we observe that when 2i becomes sufficiently large such that (1-l) ²ⁱ becomes almost zero, then we can use the simplified formula. 
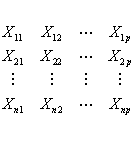
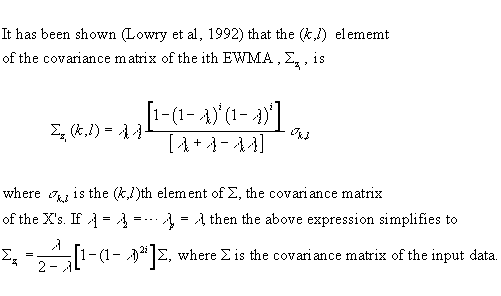
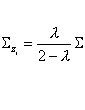
The following table gives the values of (1-l) ²ⁱ  for selected values of l and i.  It should be pointed out that a well meaning computer program does not have to adher to the simplied formula, and potential inaccuracies for low values for l and i can thus be avoided. 

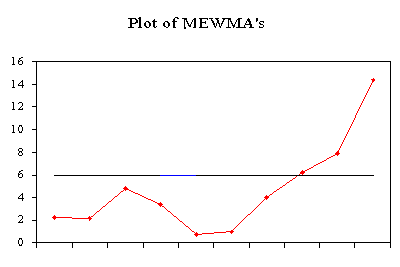
Here is an example of the application of an MEWMA control chart. To faciltate comparison with existing literature we used data from Lowry etal. 
The data was simulated from a bivariate normal distribution with unit variances and a correlation coefficient of .5. The value for l = .10 and the values for T2i were obtained by the equation given above. The covariance of the mewma vectors was obtained by using the non-simplified equation. 
That means that for every of the i mewma control statistic, the computer computed a covariance matrix , where i = 1, 2, ...10.The results of the computer routine are: 

  ***************************************************** 
 *      Multi-Variate EWMA Control Chart             *    ****************************************************** 

   DATA SERIES           MEWMA Vector           MEWMA 
     1         2           1         2        STATISTIC 
 -1.190     0.590      -0.119     0.059         2.1886 
  0.120     0.900      -0.095     0.143         2.0697 
 -1.690     0.400      -0.255     0.169         4.8365 
  0.300     0.460      -0.199     0.198         3.4158 
  0.890    -0.750      -0.090     0.103         0.7089 
  0.820     0.980       0.001     0.191         0.9268 
 -0.300     2.280      -0.029     0.400         4.0018 
  0.630     1.750       0.037     0.535         6.1657 
  1.560     1.580       0.189     0.639         7.8554 
  1.460     3.050       0.316     0.880        14.4158 

 VEC    XBAR       MSE      Lamda 
  1     .260      1.200     0.100 
  2    1.124      1.774     0.100 

 The UCL = 5.938  for a = .05 

   

 .